
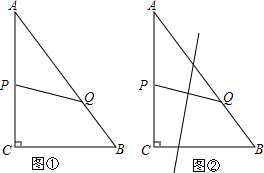
分析 (1)如图1所示,过点Q作QM⊥AC,垂足为M.先由勾股定理求得AB的长,然后由平行线分线段成比例定理求得AM、QM的长,从而求得PM的长,最后在Rt△QPM中,由勾股定理求得PQ长即可;
(2)①当△APQ∽△ACB时,依据相似三角形的性质可求得t=$\frac{20}{9}$;②当△APQ∽△ABC时.依据相似三角形的性质可求得t=$\frac{25}{9}$;
(3)当点P在AC上时,如图2所示:过点Q作QM⊥AC,垂足为M,先表示出MQ的长,然后由三角形的面积公式可求得函数的关系式;当点P在BC上时,如图3所示,过点P作PN⊥AB,垂足为N.先求得PN的长,最后由三角形的面积公式可求得函数的关系式;
(4)图4、图5、图6所示,分为PC=CQ、AP=AQ、BP=BQ三种情况,然后根据线段相等列方程求解即可.
解答 解:(1)如图1所示,过点Q作QM⊥AC,垂足为M.在△PMQ中
在Rt△ABC中,由勾股定理得:AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵t=1,
∴AP=1,QB=1.
∴AQ=4.
∵QM⊥AC,BC⊥AC,
∴QM∥BC.
∴$\frac{AQ}{AB}=\frac{AM}{AC}$=$\frac{MQ}{CB}$,即$\frac{4}{5}=\frac{AM}{4}$=$\frac{MQ}{3}$.
∴AM=$\frac{16}{5}$,MQ=$\frac{12}{5}$.
∴PM=$\frac{11}{5}$.
在Rt△QPM中,由勾股定理得:PQ=$\sqrt{P{M}^{2}+Q{M}^{2}}$=$\frac{\sqrt{265}}{5}$.
(2)①当△APQ∽△ACB时.
∵△APQ∽△ACB,
∴$\frac{AP}{AC}=\frac{AQ}{AB}$.
∴$\frac{t}{4}=\frac{5-t}{5}$.
解得:t=$\frac{20}{9}$.
②当△APQ∽△ABC时.
∵△APQ∽△ABC,
∴$\frac{AP}{AB}=\frac{AQ}{AC}$.
∴$\frac{t}{5}=\frac{5-t}{4}$.
解得:t=$\frac{25}{9}$.
(3)①当点P在AC上时,如图2所示:过点Q作QM⊥AC,垂足为M.
∵sin∠QAM=$\frac{3}{5}$,
∴MQ=$\frac{3}{5}$AQ=$\frac{3}{5}$(5-t).
∴△APQ的面积=$\frac{1}{2}AP•MQ$=$\frac{1}{2}t•\frac{3}{5}(5-t)$=$-\frac{3}{10}{t}^{2}+\frac{3}{2}t$.
②当点P在BC上时,如图3所示,过点P作PN⊥AB,垂足为N.
∵sin∠B=$\frac{4}{5}$,
∴PN=PB•sin∠B=$\frac{4}{5}$PB=$\frac{4}{5}$(7-t).
∴△APQ的面积=$\frac{1}{2}AQ•PN$=$\frac{1}{2}×(5-t)×\frac{4}{5}(7-t)$=$\frac{2}{5}{t}^{2}-\frac{24}{5}t+14$.
∴s与t的函数关系式为$S=\left\{\begin{array}{l}{-\frac{3}{10}{t}^{2}+\frac{3}{2}t(0<t≤4)}\\{\frac{2}{5}{t}^{2}-\frac{24}{5}t+14(4<t<5)}\end{array}\right.$.
(4)①如图4所示,当PC=CQ时,过点作QN⊥BC,垂足N.
∵sin∠B=$\frac{AC}{CB}=\frac{4}{5}$,cos∠B=$\frac{BC}{AB}$=$\frac{3}{5}$,
∴QN=$\frac{4}{5}$QB=$\frac{4}{5}t$,NB=$\frac{3}{5}$QB=$\frac{3}{5}t$.
∴CN=3-$\frac{3}{5}t$.
在Rt△CNQ中,CQ=$\sqrt{(\frac{4}{5}t)^{2}+(3-\frac{3}{5}t)^{2}}$.
∵CP=CQ,
∴4-t=$\sqrt{(\frac{4}{5}t)^{2}+(3-\frac{3}{5}t)^{2}}$.
解得:t=$\frac{35}{22}$.
②如图5所示,当AP=AQ时,
∵AP=t,AQ=AB-BQ=5-t,
∴t=5-t.
解得:t=2.5.
③如图6所示,当BP=BQ时,连接PB.
在Rt△PBC中,PB=$\sqrt{P{C}^{2}+B{C}^{2}}$=$\sqrt{(4-t)^{2}+{3}^{2}}$.
∵PB=QB,
∴$\sqrt{(4-t)^{2}+{3}^{2}}$=t.
解得:t=$\frac{25}{8}$.
综上所述,当t=$\frac{35}{22}$或t=2.5或t=$\frac{25}{8}$时,线段PQ的垂直平分线经过△ABC的顶点.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理的应用、等腰三角形的性质、线段垂直平分线的性质、锐角三角函数的定义、三角形的面积公式,解答本题主要应用了分类讨论的数学思想,根据题意画出符合题意得图形是解题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:解答题
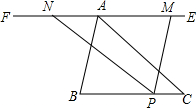 如图所示,P点是线段BC上的一点,过点A作EF∥BC,过点P分别作PM∥AB,PN∥AC,PM,PN分别交EF于M,N两点,当BP=2PC时.线段AM与AN有什么数量关系?为什么?
如图所示,P点是线段BC上的一点,过点A作EF∥BC,过点P分别作PM∥AB,PN∥AC,PM,PN分别交EF于M,N两点,当BP=2PC时.线段AM与AN有什么数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
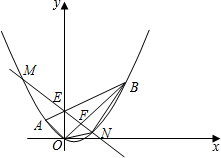 如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
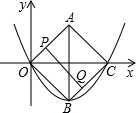 已知:四边形AOBC是正方形,C点的坐标是$(4\sqrt{2},0)$,动点P、Q同时从O点出发,P沿折线OACB的方向运动,Q沿折线OBCA的方向运动.若P的运动速度是每秒1个单位长度,Q的运动速度是每秒2个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,则S与t之间的函数图象大致是( )
已知:四边形AOBC是正方形,C点的坐标是$(4\sqrt{2},0)$,动点P、Q同时从O点出发,P沿折线OACB的方向运动,Q沿折线OBCA的方向运动.若P的运动速度是每秒1个单位长度,Q的运动速度是每秒2个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,则S与t之间的函数图象大致是( )| A. | 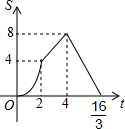 | B. | 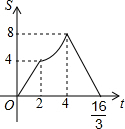 | C. | 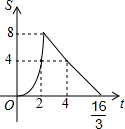 | D. | 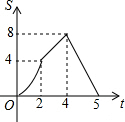 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,
如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 中国数字音乐销售额/亿元 | 15.2 | 16.5 | 17.9 | 19.5 | 21.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
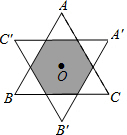 如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.
如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com