
| b |
| 2a |
| 4ac-b2 |
| 4a |
| -2 |
| 2×1 |
| 4×1×3-42 |
| 4×1 |
| 6 |
| 2×(-3) |
| 4×(-3)×2-62 |
| 4×(-3) |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
 (2011•安宁市一模)在如图所示的方格纸中,每个小正方形的边长都为1.
(2011•安宁市一模)在如图所示的方格纸中,每个小正方形的边长都为1.| m | x |
查看答案和解析>>
科目:初中数学 来源:海南省中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
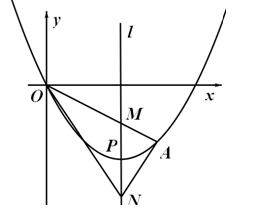
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,
 OA交其对称轴
OA交其对称轴![]() 于点M,点M、N关于点P对称,连接AN、ON
于点M,点M、N关于点P对称,连接AN、ON
(1)求该二次函数的关系式.
(2)若点A的坐标是(6,-3),求△ANO的面积.
(3)当点A在对称轴![]() 右侧的二次函数图象上运动,请解答下列问题:
右侧的二次函数图象上运动,请解答下列问题:
①证明:∠ANM=∠ONM
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(海南省I卷)数学(带解析) 题型:解答题
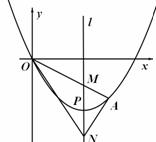
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,
OA交其对称轴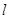 于点M,点M、N关于点P对称,连接AN、ON
于点M,点M、N关于点P对称,连接AN、ON
(1)求该二次函数的关系式.
(2)若点A的坐标是(6,-3),求△ANO的面积.
(3)当点A在对称轴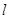 右侧的二次函数图象上运动,请解答下列问题:
右侧的二次函数图象上运动,请解答下列问题:
①证明:∠ANM=∠ONM
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.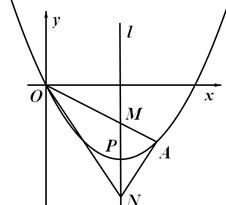
查看答案和解析>>
科目:初中数学 来源:2012年云南省昆明市中考数学模拟试卷(解析版) 题型:解答题
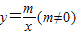 的图象的一支恰好经过点C2,求此反比例函数解析式.
的图象的一支恰好经过点C2,求此反比例函数解析式.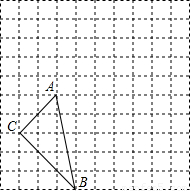
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com