
【题目】如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到![]() ,
,![]() ).
).
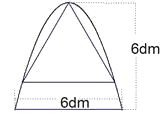
【答案】5.2dm.
【解析】
以抛物线的顶点O为坐标原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴,建立平面直角坐标系,设抛物线解析式为y=ax2(a≠0),利用已知数据求出a的值,再利用等边三角形的性质计算即可.
解:以抛物线的顶点O为坐标原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴,建立平面直角坐标系.
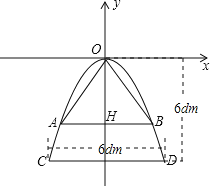
则D(3,-6)
设抛物线解析式为y=ax2(a≠0),
∵D(3,-6)在抛物线上代入得:a=![]() ,
,
∴y=![]() x2,
x2,
∵△ABO是等边三角形,
∴OH=![]() BH,
BH,
设B(x,![]() x),
x),
∴![]() x=
x=![]() x2,
x2,
∴x1=0(舍),x2=![]() ,
,
∴BH=![]() ,AB=3
,AB=3![]() ≈5.2(dm),
≈5.2(dm),
答:等边三角形的边长为5.2dm


科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
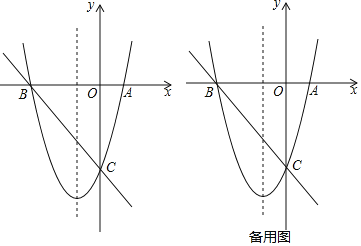
(1)求抛物线的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD申CD边上任意一点.
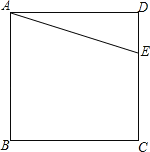
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A ,B ,C ,CD= ;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF,若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
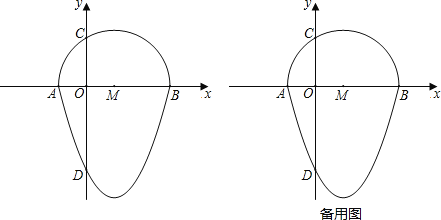
查看答案和解析>>
科目:初中数学 来源: 题型:
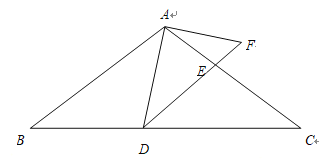
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为![]() 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为![]() 万元/辆时,平均每周售出
万元/辆时,平均每周售出![]() 辆;售价每降低
辆;售价每降低![]() 万元,平均每周多售出
万元,平均每周多售出![]() 辆.
辆.
(1)当售价为![]() 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;
(2)若该店计划平均每周的销售利润是![]() 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com