
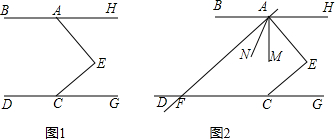
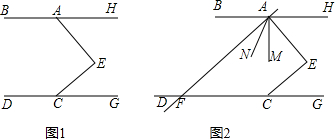
如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE, .
.
(1)求证:BH∥CD;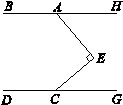
(2)如图:直线AF交DC于F,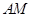 平分∠EAF,
平分∠EAF, 平分∠BAE. 试探究∠
平分∠BAE. 试探究∠ ,∠AFG的数量关系.
,∠AFG的数量关系.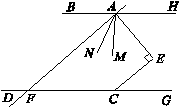
(1)延长AE交DC于点F,根据三角形外角的性质可得∠DCE=∠EFC+90°,再结合 可得∠HAE=∠EFC,即可证得结论;(2)∠MAN=
可得∠HAE=∠EFC,即可证得结论;(2)∠MAN=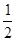 ∠AFG
∠AFG
解析试题分析:(1)延长AE交DC于点F,根据三角形外角的性质可得∠DCE=∠EFC+90°,再结合 可得∠HAE=∠EFC,即可证得结论;
可得∠HAE=∠EFC,即可证得结论;
(2)根据平行线的性质可得∠BAF=∠AFG,根据角平分线的性质可得∠MAN=∠EAN-∠EAM=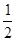 (∠BAE-∠EAF)=
(∠BAE-∠EAF)=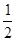 ∠BAF,即可得到结果.
∠BAF,即可得到结果.
(1)延长AE交DC于点F
∵∠DCE=∠EFC+90°,
∴∠HAE=∠EFC
∴BH∥CD;
(2)∵BH∥CD
∴∠BAF=∠AFG
∵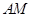 平分∠EAF,
平分∠EAF, 平分∠BAE
平分∠BAE
∴∠MAN=∠EAN-∠EAM=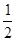 (∠BAE-∠EAF)=
(∠BAE-∠EAF)=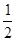 ∠BAF
∠BAF
∴∠MAN=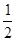 ∠AFG.
∠AFG.
考点:平行线的判定与性质,三角形外角的性质,角平分线的性质
点评:平行线的判定与性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2015届湖北省七年级5月月考数学试卷(解析版) 题型:解答题
如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,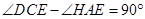 .
.
(1)求证:BH∥CD;

(2)如图:直线AF交DC于F,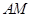 平分∠EAF,
平分∠EAF,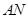 平分∠BAE. 试探究∠
平分∠BAE. 试探究∠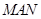 ,∠AFG的数量关系.
,∠AFG的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com