
分析 (1)根据关于x的方程x2-x-m=0有两个不相等的实数根得到△=1-4×1×(-m)>0,求出m的取值范围;
(2)根据m的取值范围可知m可取0,1,2,3,然后把m值代入原方程验证满足题意m的值.
解答 解:(1)△=1-4×1×(-m)=1+4m>0,
∴m>-$\frac{1}{4}$;
(2)∵m为小于4的整数,
∴m可取0,1,2,3.
当m=0时,△=1,方程为x2-x=0,根是整数;
当m=1时,△=5,方程的根不是整数;
当m=2时,△=9,方程为x2-x-2=0,根是整数;
当m=3时,△=13,方程的根不是整数.
综上,m的值为0或2.
点评 本题主要考查了根的判别式的知识,解答本题的关键是根据根的判别式的意义求出m的取值范围,此题难度不大.


科目:初中数学 来源: 题型:解答题
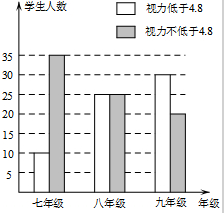 在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
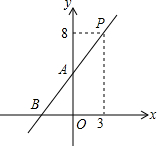 已知:如图,直线y=kx+4(k≠0)经过点A,B,P.
已知:如图,直线y=kx+4(k≠0)经过点A,B,P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )
如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com