
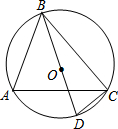
 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$.
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$. 科目:初中数学 来源: 题型:选择题
| A. | 9.8 | B. | 9.6 | C. | 9.5 | D. | 9.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型汽车 | B型汽车 | |
| 满载量(吨) | 5 | 4 |
| 费用(元)/次 | 800 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
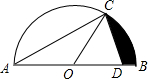 如图,AB是半圆O的直径,点C在半圆上,点D在AB上,且AC=AD,OC=2,∠CAB=30°.
如图,AB是半圆O的直径,点C在半圆上,点D在AB上,且AC=AD,OC=2,∠CAB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
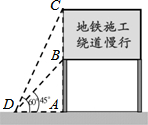 2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
2014年1月3日,长沙轨道交通3号线一期工程正式开工建设,交警队计划在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com