
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高发现电线杆 AB 的影子落在土坡的坡面CD和地面 BC上,量得 CD= 12 米 , BC= 20 米 ,CD与地面成30°角,且此时测得1米杆的影长为2 米,求电线杆的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
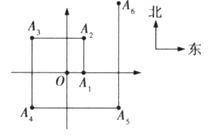
【题目】如图,一个机器人从点O出发,向正东方向走3m到达点![]() ,再向正北方向走6m到达点
,再向正北方向走6m到达点![]() ,再向正西方向走9m到达点
,再向正西方向走9m到达点![]() ,再向正南方向走12m到达点
,再向正南方向走12m到达点![]() ,再向正东方向走15m到达点
,再向正东方向走15m到达点![]() ,按如此规律走下去,当机器人走到点
,按如此规律走下去,当机器人走到点![]() 时,点
时,点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
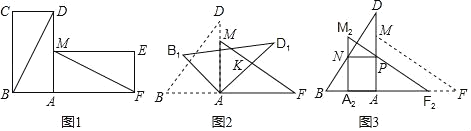
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形
(1)概念理解
①根据上述定义举一个等补四边形的例子:
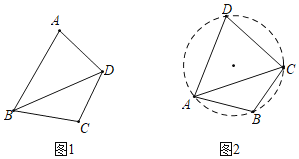
②如图1,四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:四边形ABCD是等补四边形
(2)性质探究:
③小明在探究时发现,由于等补四边形有一组对角互补,可得等补四边形的四个顶点共圆,如图2,等补四边形ABCD内接于⊙O,AB=AD,则∠ACD ∠ACB(填“>”“<”或“=“);
④若将两条相等的邻边叫做等补四边形的“等边”,等边所夹的角叫做“等边角”,它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”,请用语言表述③中结论:
(3)问题解决
在等补四边形ABCD中,AB=BC=2,等边角∠ABC=120°,等补对角线BD与等边垂直,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
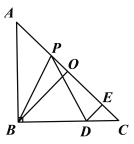
【题目】如图所示,在等腰直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为点E,求证:PE=BO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com