
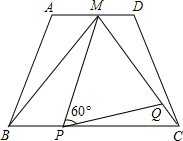
 如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.分析 (1)根据等腰梯形的性质证明△AMB≌△DMC,得到AB=DC,得到答案;
(2)①作QH⊥PC于H,证明△MBP∽△PCQ,根据相似三角形的性质得到比例式求出CQ的长,根据余弦的定义求出答案;
②证明△MBP∽△PCQ,根据相似三角形的性质得到比例式,表示出y与x的关系,得到函数关系式,根据三角形面积公式计算即可.
解答 (1)证明:∵△MBC是等边三角形,
∴MB=MC,∠MBC=∠MCB=60°,
∵M是AD的中点,
∴AM=MD,
∵AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠MCB=60°,
在△AMB和△DMC中,
$\left\{\begin{array}{l}{AM=DM}\\{∠AMB=∠DMC}\\{MB=MC}\end{array}\right.$,
∴△AMB≌△DMC,
∴AB=DC,
∴梯形ABCD是等腰梯形;
(2)①作QH⊥PC于H,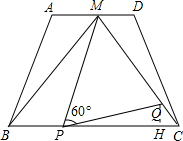
∵∠MPC=∠MBP+∠BMP=∠MPQ+∠CPQ,
∴∠BMP=∠CPQ,又∠MBP=∠MPQ=60°,
∴△MBP∽△PCQ,
∴$\frac{MB}{PC}$=$\frac{BP}{CQ}$,即CQ=$\frac{3}{4}$,
∵∠QCH=60°,
∴HC=$\frac{3}{8}$,QH=$\frac{3\sqrt{3}}{8}$,
∴PH=3-$\frac{3}{8}$=$\frac{21}{8}$,PQ=$\frac{3\sqrt{13}}{4}$,
∴cos∠CPQ=$\frac{PH}{PQ}$=$\frac{7\sqrt{13}}{26}$;
②∵MB=MC=BC=4,∠MBC=∠MCB=60°,∠MPQ=60°,
∴∠BMP+∠BPM=∠BPM+∠QPC=120°,
∴∠BMP=∠QPC,
∴△MBP∽△PCQ,
∴$\frac{PC}{BM}$=$\frac{CQ}{BP}$,
∵PC=x,MQ=y,则BP=4-x,CQ=4-y,
∴$\frac{x}{4}$=$\frac{4-y}{4-x}$,
∴y=$\frac{1}{4}$x2-x+4,
∵y=$\frac{1}{4}$x2-x+4=$\frac{1}{4}$(x-2)2+3,
∴当x=2时,y的最小值是3,
则CQ=1,QH=$\frac{\sqrt{3}}{2}$,
∴△PQC的面积=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是等腰梯形的性质、锐角三角函数的概念、相似三角形的判定和性质以及二次函数的性质,掌握相关定理并能灵活运用是解题的关键.


科目:初中数学 来源: 题型:解答题
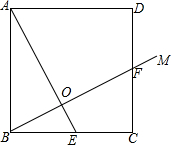 已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
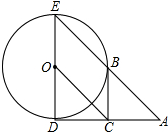 如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.
如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
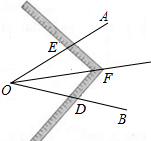 工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )
工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
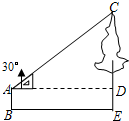 如图,小颖利用有一锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE=6m,她的眼睛距地面的距离AB=1.5m,那么这棵树高( )
如图,小颖利用有一锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE=6m,她的眼睛距地面的距离AB=1.5m,那么这棵树高( )| A. | 2$\sqrt{3}$m | B. | (2$\sqrt{3}+1.5$)m | C. | (3$\sqrt{2}+1.5$)m | D. | 4.5m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com