练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是（　　）

    A. 6 B. 5 C. 4 D. 3

    B 【解析】试题分析：过O作OC⊥AB于C，根据垂径定理求出AC=BC=AB=12，在Rt△AOC中，由勾股定理得：OC==5． 故选：B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，在△ABC中,∠B=45°, ，等腰直角△DAE中，∠DAE=90°，且点D是边BC上一点。

    (1)求AC的长；

    (2)如图1，当点E恰在AC上时,求点E到BC的距离；

    (3)如图2, 当点D从点B向点C运动时，求点E到BC的距离的最大值。

    图1 图2

    (1)4(2) (3) 【解析】试题分析：（1）作AF⊥BC，垂足为F，由已知可得BF=AF=2，从而得CF=BC-BF=2，在Rt△FAC中，利用勾股定理即可求出AC长； （2）过点A作AB的垂线交BC于点G，连接EG，证明△BAD≌△GAE，从而得∠AGE=∠ABD=45°，EG=BD，继而得∠EGB=90°，得到点E到BC的距离为EG的长，设BD=x，则DF=2-x，CD=2+2...

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型：单选题

    一个两位数，个位数字为a，十位数字为b，把这个两位数的个位数字与十位数字交换，得到一个新的两位数，则新两位数与原两位数的和为

    A. B. C. D.

    D 【解析】试题解析：根据题意得：（10a+b）+（10b+a）=10a+b+10b+a=11a+11b． 故选D.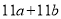

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：解答题

    计算：

    （1） 2cos30°－ －2 （2）(－ ) (+)

    (1)－2 (2)1 【解析】试题分析：（1）先对二次根式、三角函数值进行运算，然后进行乘法运算，最后进行减法运算即可；（2）用平方差公式将式子展开计算即可. 试题解析： （1）2cos30°－ －2=2×－×3－2=－2； （2）(－ ) (+)=3－2=1.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，⊙O的直径AB=2，弦AC=1，点D在⊙O上，则∠D的度数是（ ）

    A. 30° B. 45° C. 60° D. 75°

    C 【解析】试题分析：由⊙O的直径是AB，得到∠ACB=90°，根据特殊三角函数值可以求得∠B的值，继而求得∠A和∠D的值． 【解析】 ∵⊙O的直径是AB， ∴∠ACB=90°， 又∵AB=2，弦AC=1， ∴sin∠CBA=， ∴∠CBA=30°， ∴∠A=∠D=60°， 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    若直角三角形两条直角边长分别为5和12，则斜边上的中线长为（ ）

    A. 13 B. 6 C. 6.5 D. 5

    C 【解析】斜边长为： =13，所以斜边上的中线长为：6.5. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型：解答题

    解方程:

    x=2 【解析】试题分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解． 试题解析：方程两边同乘x（x﹣1），得x2﹣x2+x=2x﹣2， 整理，得﹣x=﹣2， 解得，x=2， 检验：当x=2时，x（x﹣1）=2≠0， 则x=2是原分式方程的解．

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型：单选题

    下列计算中，正确的是（　　）

    A. x3•x2=x4 B. （x+y）（x﹣y）=x2+y2

    C. x（x﹣2）=﹣2x+x2 D. 3x3y2÷xy2=3x4

    C 【解析】试题解析：A、结果是x5，故本选项不符合题意； B、结果是x2-y2，故本选项不符合题意； C、结果是-2x+x2，故本选项符合题意； D、结果是3x2，故本选项不符合题意； 故选C．

    查看答案和解析>>

    科目：初中数学 来源：云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    若，则x的取值范围是______ ．

    或 【解析】【解析】 原式可化为① 和②，解①得x＞3，解②得x＜﹣2． 故答案为：x＞3或x＜﹣2．

    查看答案和解析>>

    同步练习册答案