如图.根据图中的数据求解下列各题:(1)请计算阴影部分的面积,(2)当a=15.b=20时.求阴影部分的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

2．

如图，根据图中的数据求解下列各题：
（1）请计算阴影部分的面积（单位：厘米）；
（2）当a=15，b=20时，求阴影部分的面积．

分析（1）分别表示出矩形的长和宽，利用矩形的面积计算方法即可表示出阴影部分的面积；
（2）代入两个未知数的值后求代数式的值即可．

解答解：（1）根据图形得：矩形的两边长分别为（a-6）和（b-10），
所以阴影部分的面积为（a-6）×（b-10）=ab-10a-6b+60；

（2）当a=15，b=20时，阴影部分的面积为：9×10=90平方厘米．

点评本题考查了列代数式及代数式求值的知识，了解矩形的面积方法并能表示出该矩形的长和宽是解答本题的关键，难度不大．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

12．

实数a，b在数轴上的位置如图所示，那么化简|a-b|-$\sqrt{a^2}$的结果是（　　）

A．

-b

B．

a²+2

C．

$\sqrt{a+2}$

D．

$\sqrt{{a^2}+2}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

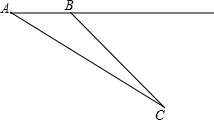随着课程改革的不断深入，对话交流、师生共同探索已成课堂常态，下面的问题取自课堂实录：（在本题计算中sin37°=$\frac{3}{5}$，cos37°=$\frac{4}{5}$，tan37°=$\frac{3}{4}$，cot37°=$\frac{4}{3}$）
老师首先给出（1）：如图，在一次直行中观察道路一边的某建筑物C，在A点处观察到看该建筑物的视线和公路的夹角为37°，继续直行50米到达B后发现看该建筑物的视线和公路的夹角变成了45°，求该建筑物C离开公路的距离（请你一起完成）
然后老师又给出变式（2）：如果我们在上述问题中删去“如图”两个字，其它不变，这时，问题的答案是否有变化？如果有变化，请画出草图并求出答案（请你一起完成）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．2002²⁰¹⁶的末位数字是多少？为了解决这个问题，不妨从特殊数的幂的个位数字中发现规律：
2¹=2，2²=4，2³=8，2⁴=16，
2⁵=2⁴⁺¹=32，2⁶=2⁴⁺²=64，2⁷=2⁴⁺³=128，2⁸=2⁴⁺⁴=258．
2^4k+1个位数字为2，2^4k+2个位数字为4，2^4k+3个位数字为8，2^4（k+1）个位数字为6．
从上述数据中发现，底数为2，指数分别为（4k+1），（4k+2），（4k+3），4k+4时，幂的末位数分别为2，4，8，6，又2002²⁰¹⁶=2002^4×504=2^4×504×1001^4×504，因此它与2⁴的个位数字相同；幂2002²⁰¹⁶的末位数字是6．
你能推出3²⁰¹⁵个位上的数字是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

17．多项式4-x²+2x³-x⁴分解因式的结果是（2-x）（x+1）（x²-x+2）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

如图所示，一次函数的图象与x轴、y轴分别相交于A，B两点，如果点A的坐标为（4，0），且OA=2OB，试求一次函数的解析式．