
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
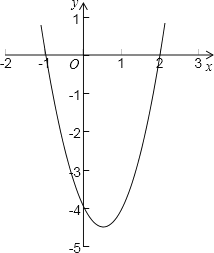
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
【答案】![]()
【解析】利用列表法作出所有等可能的情况,然后据二次函数图象上点的坐标特征求出落在抛物线与x轴围成的区域内的点的个数,再根据概率公式列式计算即可得解.
解:列表如下:
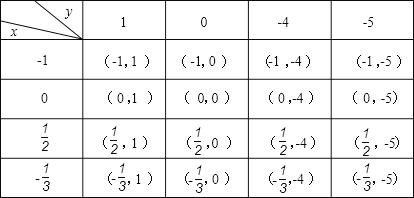
当x=-1时,y=2x2-2x-4=2×(-1)2-2×(-1)-4=2+2-4=0,
所以,没有点落在抛物线与x轴围成的区域内,
当x=0时,y=-4,
所以,没有点落在抛物线与x轴围成的区域内,
当x=![]() 时,y=2x2-2x-4=2×(
时,y=2x2-2x-4=2×(![]() )2-2×
)2-2×![]() -4=
-4=![]() -1-4=-4
-1-4=-4![]() ,
,
所以,点(![]() ,-4)落在抛物线与x轴围成的区域内,当x=-
,-4)落在抛物线与x轴围成的区域内,当x=-![]() 时,y=2x2-2x-4=2×(-
时,y=2x2-2x-4=2×(-![]() )2-2×(-
)2-2×(-![]() )-4=
)-4=![]() +
+![]() -4=-3
-4=-3![]() ,
,
所以,没有点落在抛物线与x轴围成的区域内,
综上所述,点P一共有16种情况,落在抛物线与x轴围成的区域内的点只有(![]() ,-4)一个,
,-4)一个,
所以P(落在抛物线与x轴围成的区域内)=![]() .
.
故答案为:![]() .
.
本题考查了列表法以及概率公式,用到的知识点为:概率=所求情况数与总情况数之比.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
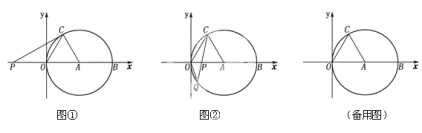
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
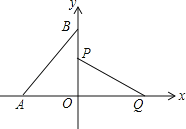
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=![]() ,那么当点P运动一周时,点Q运动的总路程为__________.
,那么当点P运动一周时,点Q运动的总路程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )

A. ∠ABD=∠C B. ∠ADB=∠ABC C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包河区发展农业经济产业,在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元![]() ,如果在未来40天葡萄的销售单价
,如果在未来40天葡萄的销售单价![]() (元
(元![]() )与时间
)与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: ,且葡萄的日销售量
,且葡萄的日销售量![]() (千克)与时间
(千克)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
(1)请直接写出![]() 与
与![]() 之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
(2)在后20天(即![]() ),请求出哪一天的日销售利润最大?日销售利润最大为多少?
),请求出哪一天的日销售利润最大?日销售利润最大为多少?
(3)在实际销售的前20天中,李大爷决定每销售1千克水果就捐赠![]() 元利润(
元利润(![]() )给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间
)给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,请求出
的增大而增大,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
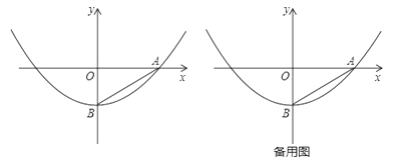
【题目】如图,在平面直角坐标系xOy中,Rt△AOB的直角边OA在x轴正半轴上,OB在y轴负半轴上,且OA=![]() ,OB=1,以点B为顶点的抛物线经过点A.
,OB=1,以点B为顶点的抛物线经过点A.
(1)求出该抛物线的解析式.
(2)第二象限内的点M,是经过原点且平分Rt△AOB面积的直线上一点.若OM=2,请判断点M是否在(1)中的抛物线上?并说明理由.
(3)点P是经过点B且与坐标轴不平行的直线l上一点.请你探究:当直线l绕点B任意旋转(不与坐标轴平行或重合)时,是否存在这样的直线l,在直线l上能找到点P,使△PAB与Rt△AOB相似(相似比不为1)?若存在,求出直线l的解析式;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com