
分析 (1)利用“m和点”的定义和等边三角形的性质得出AC,BC的长,计算即可;
(2)利用“m和点”的定义,根据已知分类讨论可得结果;
(3)根据正方形的性质得出CO=C′O=BO=AO=2,利用勾股定理可得正方形的边长.
解答 解:(1)∵点A(-2,0),B(2,0),
∴AB=4,
∵△ABC为等边三角形,
∴AC=BC=AB=4,
∴m=AC+BC=8;
(2)设E点坐标为(x,0),
∵点E是点A,B的“5和点”,
∴若点E在A的左侧,则有(-2-x)+(2-x)=5,
解得:x=-2.5;
若点E在B的右侧,则有[x-(-2)]+(x-2)=5,
解得:x=2.5;
∴E(-2.5,0),或E(2.5,0),
故答案为:(-2.5,0),或E(2.5,0);
(3)∵若点C为点A,B的“m和点”,且点C和C′在y轴上,ACBC′组成正方形,
∴AB,CC′是正方形的对角线,
∴CO=C′O=BO=AO=2,
∴BC=$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$,
∴正方形的边长为2$\sqrt{2}$.
点评 本题主要考查了等边三角形的性质和正方形的性质,运用新定义,分类讨论是解答此题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 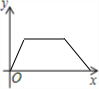 | C. | 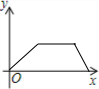 | D. | 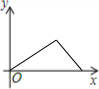 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一块长方形的土地,长40米,宽30米,在这块土地上修两条宽a米的小路,如图所示,请用代数式表示剩下土地的面积.若a=2米时,求剩下土地的面积是多少?
有一块长方形的土地,长40米,宽30米,在这块土地上修两条宽a米的小路,如图所示,请用代数式表示剩下土地的面积.若a=2米时,求剩下土地的面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com