
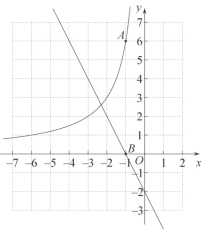
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校举行“校园谜语大赛”,比赛结束后,组织者将所有参赛选手的比赛成绩(得分均为5的倍数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
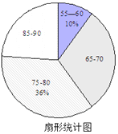
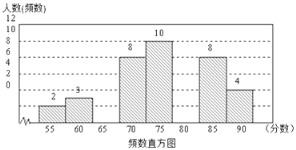
(1)本次比赛参赛选手共有 人,其中![]() 分有 人,
分有 人,![]() 分有 人;
分有 人;
(2)赛前规定,成绩达到平均分的参赛选手即可获奖.某参赛选手的比赛成绩为75分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
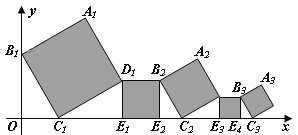
【题目】如图,在平面直角坐标系中放置5个正方形,点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O﹦60,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
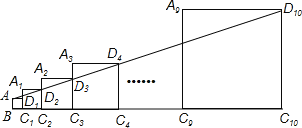
【题目】已知正方形ABCD的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3…,D10都在同一直线上,则正方形A2C2C3D3的边长是___,正方形AnnCn+1Dn+1的边长是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
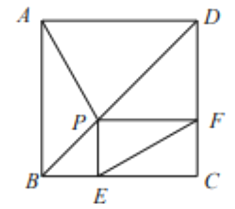
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=![]() EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
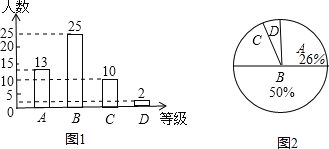
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
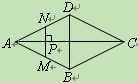
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜基地为选出适应市场需求的西红柿秧苗,在条件基本相同的情况下,将甲、乙两个品种的西红柿秧苗各500株种植在同一个大棚.对市场最为关注的产量进行了抽样调查,随机从甲、乙两个品种的西红柿秧苗中各收集了50株秧苗上的挂果数(西红柿的个数),并对数据(个数)进行整理、描述和分析,下面给出了部分信息.
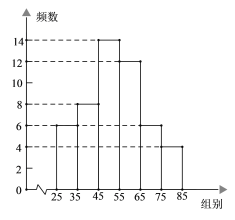
a. 甲品种挂果数频数分布直方图(数据分成6组:25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85).
b. 甲品种挂果数在45≤x<55这一组的是:
45,45,46,47,47,49,49,49,49,50,50,51,51,54
c. 甲、乙品种挂果数的平均数、中位数、众数如下:
品种 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 49.4 | m | 49 | 1944.2 |
乙 | 48.6 | 48.5 | 47 | 3047 |
根据以上信息,回答下列问题:
(1)表中m= ;
(2)试估计甲品种挂果数超过49个的西红柿秧苗的数量;
(3)可以推断出 品种的西红柿秧苗更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 20 | 35 | 41 | 4 |
(1)请根据调查结果,若该校有学生![]() 人,请估计这些学生中“比较了解”垃圾分类知识的人数.
人,请估计这些学生中“比较了解”垃圾分类知识的人数.
(2)在“比较了解”的调查结果里,其中九(1)班学生共有![]() 人,其中
人,其中![]() 名男生和
名男生和![]() 名女生,在这
名女生,在这![]() 人中,打算随机选出
人中,打算随机选出![]() 位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com