
【题目】已知:△ABC中,AB=AC,∠B=α.
(1)如图1,点D,E分别在边AB,AC上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N,求证:BD+CE=BC.需补充条件∠EMN= (用含α的式子表示)补充条件后并证明;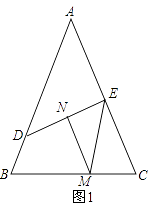
(2)把(1)中的条件改为点D,E分别在边BA、AC延长线上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N(如图2),并补充条件∠EMN=(用含α的式子表示),通过观察或测量,猜想线段BD,CE与BC之间满足的数量关系,并予以证明.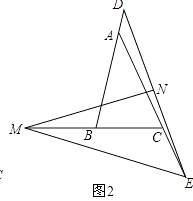
【答案】
(1)解:当∠EMN= ![]() α时,BD+CE=BC.
α时,BD+CE=BC.
理由:如图1所示:连接DM.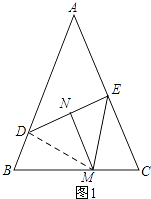
∵AB=AC,
∴∠B=∠C=α.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中,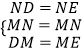 ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠DME=α.
∵∠C+∠CEM=∠DMB+∠DME,∠C=∠DME=α,
∴∠DMB=∠CEM.
在△BDM和△CME中,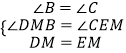 ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+MC=BC,
∴BD+EC=BC.
(2)解:当∠EMN= ![]() α时,BD=CE+BC.
α时,BD=CE+BC.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠DBM=∠MCE.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中,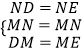 ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠EMD=∠B=α
∵∠BMD+∠MDB=α,∠EMC+∠CMD=α,
∴∠EMC=∠MDB.
在△BDM和△CME中,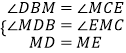 ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+BC=MC,
∴EC+BC=BD
【解析】(1)当∠EMN= ![]() α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN=
α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN= ![]() α时,BD=CE+BC.先证明∠DMN=∠EMN=
α时,BD=CE+BC.先证明∠DMN=∠EMN= ![]() α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.
α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利民种子培育基地用A、B、C三种型号的玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广.通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图(图1、图2):
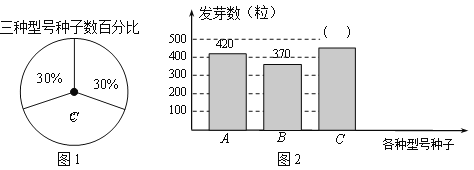
(1)C型号种子的发芽数是_________粒;
(2)直接写出应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放到一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
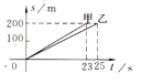
【题目】如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
(1)图象反映了哪两个变量之间的关系?
(2)他们进行的是多远的比赛?
(3)谁是冠军?
(4)乙在这次比赛中的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题:
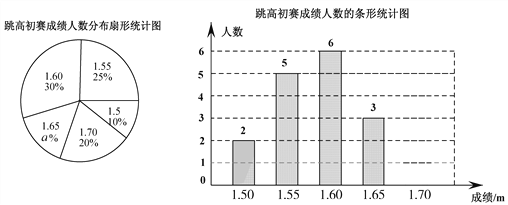
(1)扇形统计图中,初赛成绩为1.65m所在扇形图形的圆心角为_ _°;
(2)补全条形统计图;
(3)这组初赛成绩的中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠EOF,求作∠E′O′F′,使得∠E′O′F′=∠EOF,则作法的合理顺序是【 】
①以点C′为圆心,以CD的长为半径画弧,交前面的弧于点D′;②以点O为圆心,以任意长为半径画弧,交OE于点C,交OF于点D;③作射线O′E′;④以点O′为圆心,以OC的长为半径画弧,交O′E′于点C′;⑤过点D′作射线O′F′,∠E′O′F′就是所求作的角.
A. ③②①④⑤ B. ③②④①⑤
C. ②④③①⑤ D. ②③①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】集合M={x|1<x+1≤3},N={x|x2﹣2x﹣3>0},则(RM)∩(RN)等于( )
A.(﹣1,3)
B.(﹣1,0)∪(2,3)
C.(﹣1,0]∪[2,3)
D.[﹣1,0]∪(2,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com