
【题目】计算
(1)(﹣2)3+( ![]() )﹣2×22﹣(π﹣2)0
)﹣2×22﹣(π﹣2)0
(2)5x2y÷(﹣ ![]() xy)3xy2 .
xy)3xy2 .
【答案】
(1)解:(﹣2)3+( ![]() )﹣2×22﹣(π﹣2)0
)﹣2×22﹣(π﹣2)0
=﹣8+ ![]() ×4﹣0
×4﹣0
=﹣8+4×4﹣0
=8
(2)解:5x2y÷(﹣ ![]() xy)3xy2
xy)3xy2
=(5 ![]() )X2﹣1y1﹣13xy2
)X2﹣1y1﹣13xy2
=﹣10x3xy2
=﹣30x2y2
【解析】(1)先算乘方,再算加减,利用公式:(a)﹣p= ![]() (a≠0);a0=1(a≠0)(2)单项式与单项式的乘除混合运算,按从左向右的顺序进行计算,运算时注意符号.
(a≠0);a0=1(a≠0)(2)单项式与单项式的乘除混合运算,按从左向右的顺序进行计算,运算时注意符号.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握整数指数幂的运算性质(aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数))的相关知识才是答题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
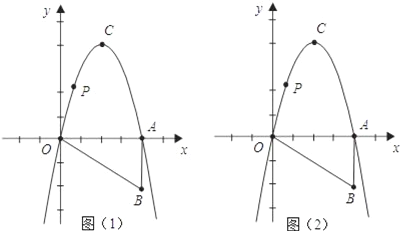
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1. 5倍.设两人出发x min后距出发点的距离为y m.图中折线段OBA表示小明在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).
(1)点B所表示的实际意义是 ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x一元二次方程x2+mx+n=0.
(1)当m=n+2时,利用根的判别式判断方程根的情况.
(2)若方程有实数根,写出一组满足条件的m,n的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在解一元二次方程时,他是这样做的:
解一元二次方程
3x2﹣8x(x﹣2)=0…第一步
3x﹣8x﹣2=0…第二步
﹣5x﹣2=0…第三步
﹣5x=2…第四步
x=﹣![]() …第五步
…第五步
(1)小明的解法从第 步开始出现错误;此题的正确结果是 .
(2)用因式分解法解方程:x(2x﹣1)=3(2x﹣1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 相似三角形一定全等B. 不相似的三角形不一定全等
C. 全等三角形不一定是相似三角形D. 全等三角形一定是相似三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b1与反比例函数y=![]() 的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,
的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,![]() ),点B坐标为(1,n).
),点B坐标为(1,n).
(1)求反比例函数及一次函数的解析式;
(2)求证:AC=BD;
(3)若将一次函数的图象上下平移若干个单位后得到y=k1x+n,其与反比例函数图象及两坐标轴的交点仍然依次为A、B、C、D.(2)中的结论还成立吗?请写出理由,对于任意k<0的直线y=kx+b.(2)中的结论还成立吗?(请直接写出结论)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com