
如图,∠1与∠C是两条直线______被第三条直线______所截构成的______角;∠2与∠B是两条直线______被第三条直线______所截构成的______角; ______被第三条直线______所截构成的______角.
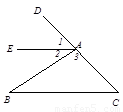
AE、BC、CD、同位角;AE、BC、AB、内错角;AB、AC、BC、同旁内角
【解析】
试题分析:根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.
∠1与∠C是两条直线AE、BC被第三条直线CD所截构成的同位角;
∠2与∠B是两条直线AE、BC被第三条直线AB所截构成的内错角;
∠B与∠C是两条直线AB、AC被第三条直线BC所截构成的同旁内角.
考点:本题考查了同位角、内错角、同旁内角的概念
点评:三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.


科目:初中数学 来源: 题型:
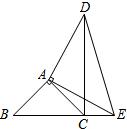 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD.有下列四个结论:
如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD.有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
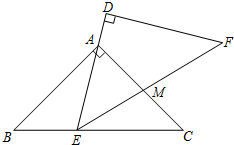 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
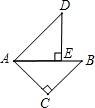 如图,△ABC与△ADE是两个全等的等腰直角三角形,∠C和∠AED都是直角.点E在AB上,如果△ABC经旋转后能与△ADE重合.那么下列说法中正确的是( )
如图,△ABC与△ADE是两个全等的等腰直角三角形,∠C和∠AED都是直角.点E在AB上,如果△ABC经旋转后能与△ADE重合.那么下列说法中正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB与BC是两条笔直的公路,B与C是两个村庄.
如图,AB与BC是两条笔直的公路,B与C是两个村庄.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com