
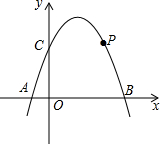
 设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.分析 (1)先根据抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0)可知x1,x2为方程的两个根,再由根与系数的关系即可得出m的值.
(2)根据勾股定理,可得AP2,PB2,再根据勾股定理的逆定理,可得关于a的方程,根据解方程,可得答案
(3)①当点P位于x轴上方时,根据轴对称的性质可得出P点坐标;
②当点P位于x轴下方时,根据CE∥AP,作PM⊥x轴于点M,四边形ACEP是平行四边形可得出△COE≌△PMA,故PM=OC=2即P点的纵坐标为-2,代入抛物线的解析式即可得出x的值,进而得出P点坐标.
解答 解:(1)∵当抛物线y=mx2-3mx+2(m≠0)和x轴相交时,y=0,即mx2-3mx+2=0,
∴x1,x2为方程的两个根,
∴x1+x2=-$\frac{-3m}{m}$=3,x1x2=$\frac{2}{m}$.
又∵x12+x22=17,
∴(x1+x2)2-2x1x2=17,
∴9-$\frac{4}{m}$=17,
∴m=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
顶点横坐标是-$\frac{b}{2a}$=-$\frac{\frac{3}{2}}{2×(-\frac{1}{2})}$=$\frac{3}{2}$,
顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{2})×2-(\frac{3}{2})^{2}}{4×(-\frac{1}{2})}$=$\frac{25}{8}$,
顶点M的坐标($\frac{3}{2}$,$\frac{25}{8}$);
(2)设P(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),
当y=0时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,
解得x1=-1,x2=4,即A(-1,0),B(4,0).
由勾股定理,得AP2=(a+1)2+(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)2,
PB2=(a-4)2+(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)2,
由勾股定理逆定理,得AP2+PB2=AB2,
即(a+1)2+(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)2+(a-4)2+(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)2=(4+1)2,
化简,得
a2-3a=0.
解得a1=0,a2=3,
P1(0,2),P2(3,2);
(3)存在这样的点P,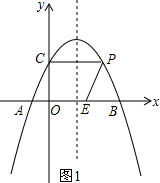 ①如图1,当点P位于x轴上方时,
①如图1,当点P位于x轴上方时,
∵PC∥AE,
∴PC∥x轴,
∴点C与点P关于抛物线的对称轴对称.
∵抛物线的对称轴为x=$\frac{3}{2}$,C(0,2),
∴P(3,2);
②如图2,当点P位于x轴下方时,
CE∥AP,作PM⊥x轴于点M,
∵四边形ACEP是平行四边形,
∴AC∥PE,AC=PE. 在△COE和△PMA中,
在△COE和△PMA中,
$\left\{\begin{array}{l}{∠COE=∠PMA}\\{∠ECO=∠APM}\\{AC=PE}\end{array}\right.$,
∴△COE≌△PMA(AAS),
∴PM=OC=2
∴P点的纵坐标为-2,代入抛物线的解析式
y=$\frac{1}{2}$x2+$\frac{3}{2}$x+2,
∴$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-2,
解得x=$\frac{3±\sqrt{41}}{2}$,
∴P( $\frac{3+\sqrt{41}}{2}$,-2)或($\frac{3-\sqrt{41}}{2}$,-2).
∴使以点A、C、P、E为顶点的四边形为平行四边形的P点有三个:(3,2),( $\frac{3+\sqrt{41}}{2}$,-2),($\frac{3-\sqrt{41}}{2}$,-2).
点评 本题考查的是二次函数综合题.
(1)利用根与系数的关系求函数解析式;
(2)利用勾股定理求三角形的边,再利用勾股定理逆定理求三角形的角;
(3)利用了平行四边形的判定与性质,全等三角形的判定与性质,自变量与函数值的对应关系,分类讨论是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
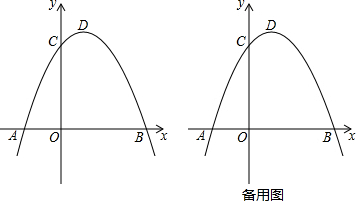
 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.
赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.| 等级 人数 科目 | A | B | C | D |
| 物理实验操作 | 120 | 7 | 90 | 20 |
| 化学实验操作 | 90 | 110 | 30 | 20 |
| 体育 | 123 | 140 | 160 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
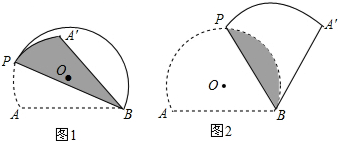
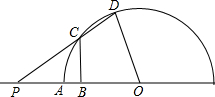 已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)
如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com