
【题目】如图1,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 是
是![]() 轴上的一点,且以
轴上的一点,且以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴玮抛物线相交于点
轴玮抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,试探究当点
,试探究当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 的面积最大,求点
的面积最大,求点![]() 的坐标及最大面积;
的坐标及最大面积;
(4)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴,
轴,![]() 轴上分别找点
轴上分别找点![]() ,
,![]() ,使四边形
,使四边形![]() 的周长最小,求出点
的周长最小,求出点![]() ,
,![]() 的坐标.
的坐标.
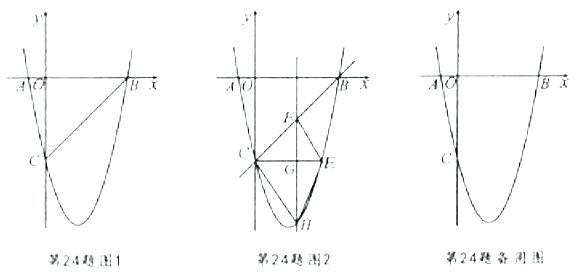
【答案】(1) y=x2﹣4x﹣5,(2) D的坐标为(0,1)或(0,![]() );(3) 当t=
);(3) 当t=![]() 时,四边形CHEF的面积最大为
时,四边形CHEF的面积最大为![]() .(4) P(
.(4) P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).
【解析】
试题分析:(1)根据待定系数法直接抛物线解析式;
(2)分两种情况,利用相似三角形的比例式即可求出点D的坐标;
(3)先求出直线BC的解析式,进而求出四边形CHEF的面积的函数关系式,即可求出最大值;
(4)利用对称性找出点P,Q的位置,进而求出P,Q的坐标.
试题解析:(1)∵点A(﹣1,0),B(5,0)在抛物线y=ax2+bx﹣5上,
∴![]() ,
,
∴![]() ,
,
∴抛物线的表达式为y=x2﹣4x﹣5,
(2)如图1,令x=0,则y=﹣5,

∴C(0,﹣5),
∴OC=OB,
∴∠OBC=∠OCB=45°,
∴AB=6,BC=5![]() ,
,
要使以B,C,D为顶点的三角形与△ABC相似,则有![]() 或
或![]() ,
,
①当![]() 时,
时,
CD=AB=6,
∴D(0,1),
②当![]() 时,
时,
∴ ,
,
∴CD=![]() ,
,
∴D(0,![]() ),
),
即:D的坐标为(0,1)或(0,![]() );
);
(3)设H(t,t2﹣4t﹣5),
∵CE∥x轴,
∴点E的纵坐标为﹣5,
∵E在抛物线上,
∴x2﹣4x﹣5=﹣5,∴x=0(舍)或x=4,
∴E(4,﹣5),
∴CE=4,
∵B(5,0),C(0,﹣5),
∴直线BC的解析式为y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣ ![]() )2+
)2+![]() ,
,
∵CE∥x轴,HF∥y轴,
∴CE⊥HF,
∴S四边形CHEF=![]() CEHF=﹣2(t﹣
CEHF=﹣2(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,四边形CHEF的面积最大为
时,四边形CHEF的面积最大为![]() .
.
(4)如图2,

∵K为抛物线的顶点,
∴K(2,﹣9),
∴K关于y轴的对称点K'(﹣2,﹣9),
∵M(4,m)在抛物线上,
∴M(4,﹣5),
∴点M关于x轴的对称点M'(4,5),
∴直线K'M'的解析式为y=![]() x﹣
x﹣![]() ,
,
∴P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).


科目:初中数学 来源: 题型:
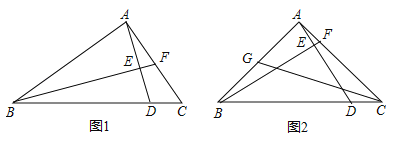
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A.端午节期间市场上粽子质量B.了解CCTV1电视剧《麦香》的收视率
C.调查我校某班学生喜欢上数学课的情况D.某品牌手机的防水性能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
A.(4,5)B.(5,4)C.(5,2)D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
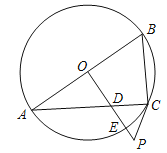
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
问题背景:已知![]() 的顶点
的顶点![]() 在
在![]() 的边
的边![]() 所在直线上(不与
所在直线上(不与![]() ,
,![]() 重合).
重合).![]() 交
交![]() 所在直线于点
所在直线于点![]() ,
,![]() 交
交![]() 所在直线于点
所在直线于点![]() .记
.记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
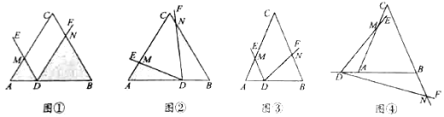
(1)初步尝试:如图①,当![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,且
,且![]() ,
,![]() 时,则
时,则![]() ;
;
(2)类比探究:在(1)的条件下,先将点![]() 沿
沿![]() 平移,使
平移,使![]() ,再将
,再将![]() 绕点
绕点![]() 旋转至如图②所示位置,求
旋转至如图②所示位置,求![]() 的值;
的值;
(3)延伸拓展:当![]() 是等腰三角形时,设
是等腰三角形时,设![]() .
.
(I)如图③,当点![]() 在线段
在线段![]() 上运动时,设
上运动时,设![]() ,
,![]() ,求
,求![]() 的表达式(结果用
的表达式(结果用![]() ,
,![]() 和
和![]() 的三角函数表示).
的三角函数表示).
(II)如图④,当点![]() 在
在![]() 的延长线上运动时,设
的延长线上运动时,设![]() ,
,![]() ,直接写出
,直接写出![]() 的表达式,不必写出解答过程.
的表达式,不必写出解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com