
【题目】如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你填空:
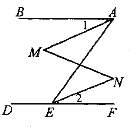
解:∵∠BAE+∠AED=180° (已知) ,
∴AB//DE( ),
∴∠BAE= ( )
又 ∵∠1=∠2(已知)
∴∠BAE-∠1= - (等式性质),
即∠MAE=∠NEA,
∴ ∥ ( ),
∴∠M=∠N(两直线平行,内错角相等).
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点C(3,1)
的图象交于点C(3,1)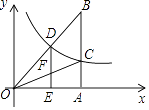
(1)试确定上述比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .求
.求![]() 的度数;
的度数;
请补全下列解法中的空缺部分.
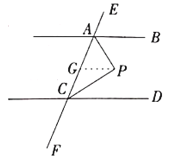
解:过点![]() 作
作![]() 交
交![]() 于点
于点![]()
∵![]() (___________)
(___________)
∴_________![]() (___________)
(___________)
∵![]() (___________)
(___________)
∴![]() ___________(___________)
___________(___________)
且![]() ______________(平行于同一直线的两直线也互相平行)
______________(平行于同一直线的两直线也互相平行)
∴![]() ____________(两直线平行,内错角相等)
____________(两直线平行,内错角相等)
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
∴![]() _____________,
_____________,
![]() _________________.(___________)
_________________.(___________)
∴![]() (___________)
(___________)
∴![]()
总结:两直线平行时,同旁内角的角平分线_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组 ![]() (a≥0),给出下列说法:
(a≥0),给出下列说法:
①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a> ![]() ;
;
③不论a取什么实数,2x+y的值始终不变;
④某直角三角形的两条直角边长分别为x+y,x﹣y,则其面积最大值为 ![]() .
.
以上说法正确的是( )
A.②③
B.①②④
C.③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).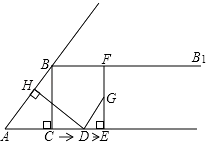
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t> ![]() 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com