
| 2 |
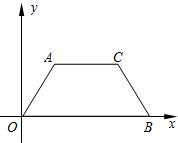 ,B(8,0).
,B(8,0).| 3 |
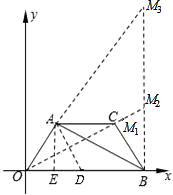
| 1 |
| 2 |
| 1 |
| 2 |
| M1B |
| OB |
| AO |
| BO |
| 3 |
| M2B |
| OB |
| AB |
| AO |
| 3 |
| 3 |
| 3 |
| M3B |
| OB |
| AO |
| AB |
8
| ||
| 3 |
8
| ||
| 3 |


科目:初中数学 来源:2011年四川省盐源县民族中学中考模拟试题数学卷 题型:填空题
如图,在等腰梯形 中,
中, ,
, ,
, ,
, =
= .直角三角板含
.直角三角板含 角的顶点
角的顶点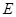 在边
在边 上移动,一直角边始终经过点
上移动,一直角边始终经过点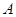 ,斜边与
,斜边与 交于点
交于点 .若
.若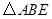 为等腰三角形,则
为等腰三角形,则 的长等于 .
的长等于 . 
查看答案和解析>>
科目:初中数学 来源:2012届江苏省盐城地区九年级上学期期末考试数学卷 题型:解答题
(本题满分12分)
如图,在等腰梯形 中,
中, ∥
∥ ,AD=AB.过
,AD=AB.过 作
作 ,交
,交 于
于 ,延长
,延长 至
至 ,使
,使 .
.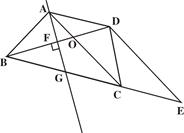
【小题1】(1)请指出四边形 的形状,并证明;
的形状,并证明;
【小题2】(2)如果 ,
, ,求三角形
,求三角形 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014届福建省晋江市八年级上学期期末跟踪测试数学试卷(解析版) 题型:解答题
如图,在等腰梯形 中,
中, ∥
∥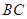 ,已知
,已知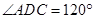 ,
,

(1)求 的度数;
的度数;
(2)若 ,
, ,试求等腰梯形
,试求等腰梯形 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com