
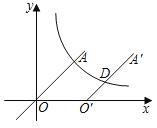
【题目】如图,正比例函数y=x的图象与反比例函数y=![]() 的图象在第一象限交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点A与点A'对应,若O'A'的中点D恰好也在该反比例函数图象上,则k的值为_____.
的图象在第一象限交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点A与点A'对应,若O'A'的中点D恰好也在该反比例函数图象上,则k的值为_____.
【答案】4
【解析】
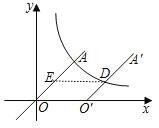
作DE∥x轴交OA于E,如图,先利用平移的性质得到OO′=3,OA=O′A′,再证明四边形OO′DE为平行四边形得到OE=O′D,接着判定OE= ![]() OA,设E(t,t),则A(2t,2t),D(t+3,t),根据反比例函数图象上点的坐标特征k=2t2t=t(t+3),然后先求出t,从而得到k的值.
OA,设E(t,t),则A(2t,2t),D(t+3,t),根据反比例函数图象上点的坐标特征k=2t2t=t(t+3),然后先求出t,从而得到k的值.
解:作DE∥x轴交OA于E,如图,
∵线段OA沿x轴向右平移3个单位长度得到线段O'A',
∴OO′=3,OA=O′A′,
∵OA∥O′A′,
∴四边形OO′DE为平行四边形,
∴OE=O′D,
∵点D为O'A'的中点,
∴O′D=![]() O′A′,
O′A′,
∴OE=![]() OA,
OA,
设E(t,t),则A(2t,2t),D(t+3,t),
∵A(2t,2t),D(t+3,t)在反比例函数y=![]() 的图象上,
的图象上,
∴k=2t2t=t(t+3),解得t=1,k=4.
故答案为4.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
最受欢迎兴趣班调查问卷 | 统计表 | |||||
选项 | 兴趣班 | 请选择 | 兴趣班 | 频数 | 频率 | |
A | 绘画 | A | 0.35 | |||
B | 音乐 | B | 18 | 0.30 | ||
C | 舞蹈 | C | 15 |
| ||
D | 跆拳道 | D | 6 | |||
你好!请选择一个(只能选一个)你最喜欢的兴趣班,在其后空格内打“√”,谢谢你的合作. |
| 1 | ||||
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从A、B、C、D四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
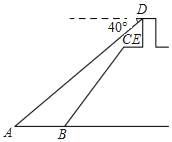
【题目】如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
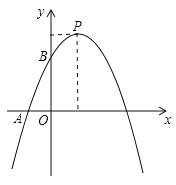
【题目】如图,已知二次函数![]() 的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
(1) 求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴与点E,联结AP交y轴与点D,若点Q、N分别为两线段PE、PD上的动点,联结QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (1)问题感知 如图1,在△ABC中,∠C=90°,且AC=BC,点P是边AC的中点,连接BP,将线段PB绕点P顺时针旋转90°到线段PD.连接AD.过点P作PE∥AB交BC于点E,则图中与△BEP全等的三角形是 ,∠BAD= °;
(2)问题拓展 如图2,在△ABC中,AC=BC=![]() AB,点P是CA延长线上一点,连接BP,将线段PB绕点P顺时针旋转到线段PD,使得∠BPD=∠C,连接AD,则线段CP与AD之间存在的数量关系为CP=
AB,点P是CA延长线上一点,连接BP,将线段PB绕点P顺时针旋转到线段PD,使得∠BPD=∠C,连接AD,则线段CP与AD之间存在的数量关系为CP=![]() AD,请给予证明;
AD,请给予证明;
(3)问题解决 如图3,在△ABC中,AC=BC=AB=2,点P在直线AC上,且∠APB=30°,将线段PB绕点P顺时针旋转60°到线段PD,连接AD,请直接写出△ADP的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 和
和![]() 的正方形如图放置(图1),其未叠合部分(阴影)面积为
的正方形如图放置(图1),其未叠合部分(阴影)面积为![]() ;若再在图1中大正方形的右下角摆放一个边长为
;若再在图1中大正方形的右下角摆放一个边长为![]() 的小正方形(如图2),两个小正方形叠合部分(阴影)面积为
的小正方形(如图2),两个小正方形叠合部分(阴影)面积为![]() .
.



(1)用含![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,求出图3中阴影部分的面积
时,求出图3中阴影部分的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( ).
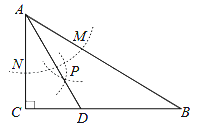
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
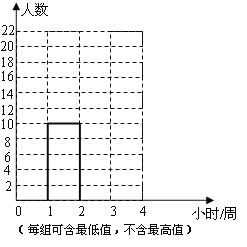
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com