
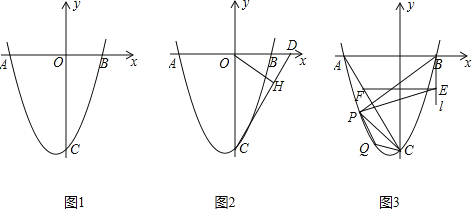
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
【答案】(1)y=x2+x﹣6;(2)OH+![]() HC的最小值为3
HC的最小值为3![]() ;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
【解析】
(1)把交点坐标代入抛物线交点式表达式,即可求解;
(2)作点O关于直线BC的对称点O′,过点O′作O′G⊥y轴交DC与点H、交y轴与点G,在图示的位置时,OH+![]() HC为最小值,即可求解;
HC为最小值,即可求解;
(3)①PE=CF,则PEcosβ=SFcosβ,即:PE=FS,即可求解;②求出HP所在的直线表达式与二次函数联立,求得交点即可.
解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2)=(x+3)(x﹣2)=x2+x﹣6,
抛物线的表达式为:y=x2+x﹣6…①,
(2)作点O关于直线DC的对称点O′交CD于点M,过点O′作O′G⊥y轴交DC与点H、交y轴与点G,
∵OD=2![]() ,OC=6,则∠OCD=30°,∴GH=
,OC=6,则∠OCD=30°,∴GH=![]() HC,
HC,
在图示的位置时,OH+![]() HC=GH+OH,此时为最小值,长度为GO′,
HC=GH+OH,此时为最小值,长度为GO′,
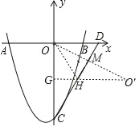
∵O′O⊥DC,∴∠OO′H=∠OCD=30°,
∴OM=![]() OC=3=
OC=3=![]() OO′,
OO′,
在Rt△OO′G中,GO′=OO′cos∠OO′G=6cos30°=3![]() ,
,
即:OH+![]() HC的最小值为3
HC的最小值为3![]() ;
;
(3)①设点P的坐标为(m,n),n=m2+m﹣6,
直线AC表达式的k值为﹣2,则直线PE表达式的k值为![]() ,
,
设直线PE的表达式为:y=![]() x+b,
x+b,
将点P坐标代入上式并解得:b=n﹣![]() m,
m,
则点E的坐标为(2,1+n﹣![]() m),点F的坐标为(
m),点F的坐标为(![]() m﹣
m﹣![]() n﹣
n﹣![]() ,1+n﹣
,1+n﹣![]() m),
m),
过点P作x轴的平行线交直线l于点M,过点F作y轴平行线交过C点作x轴的平行线于点S,
∵AC⊥PE,∴∠EPM=∠SFC=β,

∵PE=CF,则PEcosβ=SFcosβ,即:PE=FS,
∴1+n﹣![]() m+6=2﹣m,即:2m2+3m﹣2=0,
m+6=2﹣m,即:2m2+3m﹣2=0,
解得:m=![]() 或﹣2(舍去m=
或﹣2(舍去m=![]() ),
),
故点P坐标为(﹣2,﹣4),
点E坐标为(2,﹣2);
②过点P作x轴的平行线交直线l于点M、交y轴于点R,作EN⊥PB于点N,
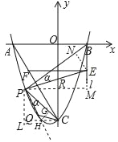
则:PM=4=BM=4,EM=BM=2,
则PE=![]() ,EN=BEsin∠NBE=2×sin45°=
,EN=BEsin∠NBE=2×sin45°=![]() ,
,
设:∠QPC=∠BPE=α,
则sin∠BPE=![]() =
=![]() =sinα,则tanα=
=sinα,则tanα=![]() ,
,
过点P作y轴的平行线交过C点与x轴的平行线于点L,延长PQ交CL于点H,过点H作HG⊥PC,
则:PL=PR=RC=CL=2,即四边形PRCL为正方形,
∴∠PCH=45°,设:GH=GC=m,
PG=![]() =3m,PC=PG+GC=4m=2
=3m,PC=PG+GC=4m=2![]() ,则m=
,则m=![]() ,
,
CH=![]() m=1,即点H坐标为(﹣1,﹣6),
m=1,即点H坐标为(﹣1,﹣6),
则HP所在的直线表达式为:y=﹣2x﹣8…②,
①②联立并解得:x=﹣1或﹣2(x=﹣2和点P重合,舍去),
故点Q的坐标为(﹣1,﹣6).
故答案为:(1)y=x2+x﹣6;(2)OH+![]() HC的最小值为3
HC的最小值为3![]() ;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
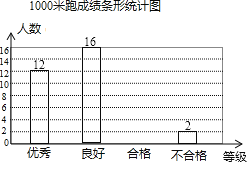
【题目】某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行100米跑步测试,按照成绩分为优秀、良好、合格与不合格四个等级,其中不合格学生占抽取学生总数的![]() ,学校绘制了如下不完整的统计图:
,学校绘制了如下不完整的统计图:
![]() 通过计算补全条形统计图;
通过计算补全条形统计图;
![]() 校九年级有300名男生,请估计其中成绩未达到良好和优秀的有多少?
校九年级有300名男生,请估计其中成绩未达到良好和优秀的有多少?
![]() 某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米跑步比赛、预赛分为A、B、C三组进行,选手由抽签确定分组,甲、乙两人恰好分在同一组的概率是多少?请画出树状图或列表加以说明.
某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米跑步比赛、预赛分为A、B、C三组进行,选手由抽签确定分组,甲、乙两人恰好分在同一组的概率是多少?请画出树状图或列表加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”,我市中小学每年都要举办一届科技运动会,下图为我市某校今年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:

(1)该校参加车模、建模比赛的人数分别是 人和 人:
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 ,并把条形统计图补充完整.
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖,今年我市中小学参加航模比赛人共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
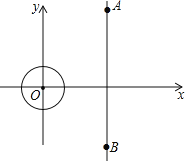
【题目】如图,在平面直角坐标系xOy中,![]() 的半径为1,A、B两点坐标分别为
的半径为1,A、B两点坐标分别为![]() 、
、![]() 已知点P是
已知点P是![]() 上的一点,点Q是线段AB上的一点,设
上的一点,点Q是线段AB上的一点,设![]() 的面积为S,当
的面积为S,当![]() 为直角三角形时,S的取值范围为______.
为直角三角形时,S的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
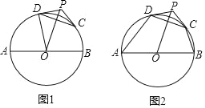
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,![]() ,垂足为
,垂足为![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上一点(不与端点重合),如果
上一点(不与端点重合),如果![]() ,下面结论:①
,下面结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
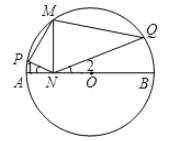
A. ①②③B. ①③⑤C. ④⑤D. ①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,以线段
,以线段![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过
,过![]() 、
、![]() 、
、![]() 三点作抛物线.
三点作抛物线.
(1)求抛物线的解析式;
(2)连结![]() ,
,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的角平分线
的角平分线![]() 交⊙
交⊙![]() 于点
于点![]() ,连结
,连结![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com