
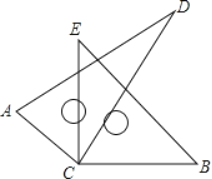
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
(1)若∠DCE=28°10',求∠ACB的度数;
(2)若∠ACB=148°21',求∠DCE的度数;
(3)直接写出∠ACB与∠DCE的数量关系.
【答案】(1)151°50'; (2)31°39'; (3)∠ACB+∠DCE=180°.
【解析】
(1)根据角的和差关系可直接得到∠ACB=90°+90°-28°10'=151°50';
(2)首先计算出∠ACE的度数,然后再根据∠ACD=90°可得∠ECD的度数;
(3)把∠ACB+∠ECD化为∠ECB+∠ACE+∠ECD,再根据∠ACD=∠ECB=90°可得∠ACB+∠DCE=180°.
(1)∵∠DCB=28°10',∠ACD=90°,
∴∠ACB=90°+90°﹣28°10'=151°50';
(2)∵∠ACB=148°21',∠ECB=90°,
∴∠ACE=148°21'﹣90°=58°21',
∵∠ACD=90°,
∴∠ECD=31°39';
(3)∠ACB+∠DCE=180°,
∵∠ACD=∠ECB=90°.
∴∠ACB+∠ECD=∠ECB+∠ACE+∠ECD=90°+90°=180°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2,则四边形PFCG的面积为_______cm2.
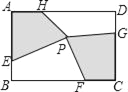
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.
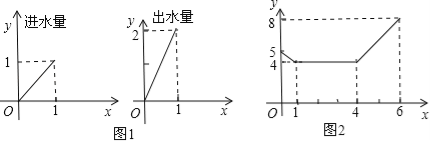
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
已知:如图,直线BC、AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∠4=∠______(______)
又∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE(等式的性质)
即∴∠3=∠______(等量代换)
∴AD∥BE(______).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,射线OP∥AE,∠AOP的角平分线交射线AE于点B.
(1)若∠A=50°,求∠ABO的度数;
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ABO-∠AOB=70°,求∠ADO的度数;
(3)如图3,若∠A=α,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,…,∠Bn-1OP的角平分线OBn,其中点B,B1,B2,…,Bn-1,Bn都在射线AE上,试求∠ABnO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+(﹣7),c=(![]() )÷
)÷![]() .
.
(1)求2[a﹣(b+c)]﹣[b﹣(a﹣2c)]的值.
(2)若A=(﹣![]() )2÷(﹣
)2÷(﹣![]() )+(1﹣
)+(1﹣![]() )2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
)2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB═![]() cm,求BC的长.
cm,求BC的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com