练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．阅读下面材料：
    在数学课上，老师提出如下问题：
    尺规作图：作直线外一点关于直线的对称点．
    已知：如图1，直线l与直线l外一点A．
    求作：直线外一点A关于直线l的对称点B．

    小颖的作法如下：
    （1）如图2，在直线l上任取点C；
    （2）以点A为圆心，AC长为半径作弧，交直线l于点D；
    （3）分别以点C，点D为圆心，AC长为半径作弧，处于直线l异侧的两弧交点为B．
    所以点B为所求．
    老师说：“小颖的作法正确．”
    请回答：小颖的作图依据是（1）四条边相等的四边形是菱形；
    （2）菱形的对角线互相垂直平分．．

    分析 根据菱形的判定以及菱形的性质解答．

    解答 解：由作图可知，AC=BC=BD=AD，
    所以，四边形ABCD是菱形，
    所以，AB⊥CD，
    小颖的作图依据是：（1）四条边相等的四边形是菱形；
    （2）菱形的对角线互相垂直平分．
    故答案为：（1）四条边相等的四边形是菱形；
    （2）菱形的对角线互相垂直平分．

    点评 本题考查了利用轴对称变换作图，主要利用了菱形的判定与性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

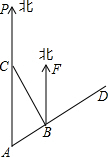    4．如图，我军两艘巡洋舰在南海某海域执行巡逻任务，两舰自A处沿AD方向航行，巡逻到B处后，1号舰沿原来的方向继续前行，2号舰则沿北偏西方向航行到C处（C在A的正北方向）后改变航线，计划沿与1号舰航线平行，且方向相同的路线航行．
    （1）用尺规在图中画出2号舰的航行路线；（保留画图痕迹，不用写作法）
    （2）若CB⊥AD，∠CBF与∠DBF的度数比为1：2，2号舰在C处的航行路线应该为北偏东多少度？并写出理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）2$\sqrt{12}-6\sqrt{\frac{1}{3}}+3\sqrt{48}$
    （2）$\sqrt{27}$÷$\sqrt{3}$-2$\sqrt{\frac{1}{5}}$×$\sqrt{10}$+$\sqrt{8}$
    （3）$（\sqrt{3}+\sqrt{2}）^{2}$-（$\sqrt{5}$+2）（$\sqrt{5}$-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．列方程解应用题．
    《算学宝鉴》全称《新集通证古今算学宝鉴》，完成于明嘉靖三年（1524年），王文素著，全书12本42卷，近50万字，代表了我国明代数学的最高水平．《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长十二步，问长阔各几何？”
    译文：一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽的各是多少步？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知关于x的一元二次方程ax2+（2+2a）x+a+2=0（a≠0）．
    （1）求证：此方程总有两个不相等的实数根；
    （2）若此方程的两个根都为整数，求整数a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．先化简，再求值：（1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4x+4}{x+1}$，其中x=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

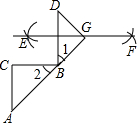    6．如图，在△ABC中，∠C=90°，DB⊥BC于点B，分别以点D和点B为圆心，以大于$\frac{1}{2}$DB的长为半径作弧，两弧相交于点E和点F，作直线EF，延长AB于点G，连接DG，下面是说明∠A=∠D的说理过程，请把下面的说理过程补充完整：
    因为DB⊥BC（已知）
    所以∠DBC=90°（垂直的定义）①
    因为∠C=90°（已知）
    所以∠DBC=∠C（等量代换）
    所以DB∥AC（内错角相等，两直线平行）②
    所以∠A=∠1③（两直线平行，同位角相等）；
    由作图法可知：直线EF是线段DB的（垂中平分线）④
    所以GD=GB，线段垂直平分线⑤（上的点到线段两端点的距离相等）
    所以∠1=∠D（等边对等角）⑥，
    因为∠A=∠E（已知）
    所以∠A=∠D（等量代换）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．一个口袋中装有3个白球、5个红球，这些球除了颜色外完全相同，充分摇匀后随机摸出一球，发现是白球
    （1）如果将这个白球放回，再摸出一球，它是白球的概率是多少？
    （2）如果将这个白球不放回，再摸出一球，它是白球的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

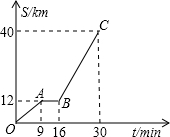    4．如图是某汽车行驶的路程s（km）与时间t（分钟） 的函数关系图．观察图中所提供的信息，解答下列问题：
    （1）求汽车在前9分钟内的平均速度．
    （2）汽车在中途停留的时间．
    （3）求该汽车行驶30千米的时间．

    查看答案和解析>>

    同步练习册答案