
【题目】如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)求证:△ABE≌△CAF
(2)如图①过A的直线与斜边BC不相交时,试探索EF、 BE、CF三条线段的关系;
(3)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求FE长.

【答案】(1)见解析;(2)EF=BE=CF.理由见解析;(3)EF的长为7.
【解析】
(1)由条件可以得出∠BAE=∠ACF,∠AEB=∠CFA,就可以得出△ABE≌△CAF;
(2)由△ABE≌△CAF就可以得出EF=BE+CF;
(3)通过证明三角形△ABE≌△CAF就可以得出结论.
(1)BAE+∠CAF=90°.
∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠FAC+∠ACF=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中
∠BAE=∠ACF∠AEB=∠CFAAB=CA
∴△ABE≌△CAF(AAS);
(2)EF=BE=CF.理由:
证明:∵△ABE≌△CAF,
∴AE=CF,BE=AF.
∵EF=AE+AF,
∴EF=CF+BE;
(3)如图2,∵∠BAC=90°,
∴∠BAF+∠CAF=90°.
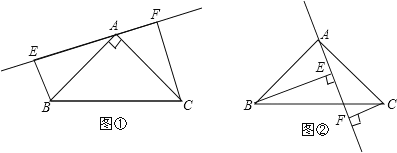
∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠FAC+∠ACF=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,
∠BAE=∠ACF∠AEB=∠CFAAB=CA,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF.
∵EF=AFAE,
∴EF=BECF=103=7.
答:EF的长为7.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF. 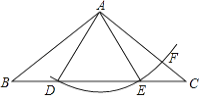
(1)求证:△ABD≌△ACE;
(2)若∠ADB=3∠CEF,请判断EF与AB有怎样的位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2![]() =2+2
=2+2![]() +1=(
+1=(![]() )2+2
)2+2![]() +1=(
+1=(![]() +1)2;
+1)2;
5+2![]() =2+2
=2+2![]() +3=(
+3=(![]() )2+2×
)2+2×![]() ×
×![]() +(
+(![]() )2=(
)2=(![]() +
+![]() )2
)2
(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2![]() ;②6+4
;②6+4![]()
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E. 
(1)求证:CE是半圆的切线;
(2)若OB=5,BC=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下: 
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共吨;
(3)调查发现,在可回收物中塑料类垃圾占 ![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( ).

A. 9 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题: 
(1)该镇本次统计的小微企业总个数是 , 扇形统计图中B类所对应扇形圆心角的度数为度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com