
【题目】数学课上,老师给出了如下问题:如图,∠AOB=80°,OC平分∠AOB,若∠BOD=20°.
(1)请你补全图形,并求∠COD的度数;
(2)若∠BOD=![]() 其他条件不变,请直接写出∠COD的度数.
其他条件不变,请直接写出∠COD的度数.

【答案】(1)60°或20°;(2)40°+β或|40°-β|.
【解析】
(1)分两种情况讨论:①当OD在OB的下方时,由OC为角平分线求出∠BOC度数,根据∠BOC+∠BOD即可求出∠COD的度数;②当OD在OB的上方时,由OC为角平分线求出∠BOC度数,根据∠BOC﹣∠BOD即可求出∠COD的度数.
(2)根据(1),类似的分两种情况讨论即可.
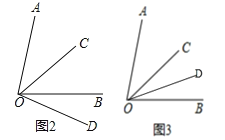
(1)分两种情况讨论:①当OD在OB的下方时,如图2.
∵OC平分∠AOB,∠AOB=80°,∴∠BOC![]() ∠AOB=40°.
∠AOB=40°.
∵∠BOD=20°,∴∠COD=∠BOC+∠BOD=40°+20°=60°.
②当OD在OB的上方时,如图3.
∵OC平分∠AOB,∠AOB=80°,∴∠BOC![]() ∠AOB=40°.
∠AOB=40°.
∵∠BOD=20°,∴∠COD=∠BOC﹣∠BOD=40°﹣20°=20°.
综上所述:∠COD的度数为60°或20°.
(2)根据(1)可得:∠COD的度数为40°+β或|40°-β|.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴为直线x=1,给出下列结论: ①b2﹣4ac>0;②2a+b=0;③abc>0;④3a+c>0,
则正确的结论个数为( )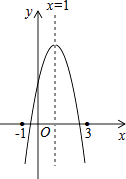
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某城镇中学学做家务的时间,一综合实践活动小组对该班50名学生进行了调查,根据调查所得的数据制成如下图的频数分布直方图.
(1)补全该图,并写出相应的频数;
(2)求第1组的频率;
(3)求该班学生每周做家务时间的平均数;
(4)你的做家务时间在哪一组内?请用一句话谈谈你的感受.
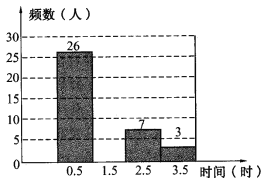
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“3·15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(2)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
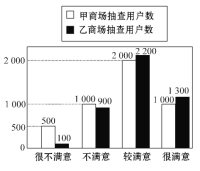
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= ![]() x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.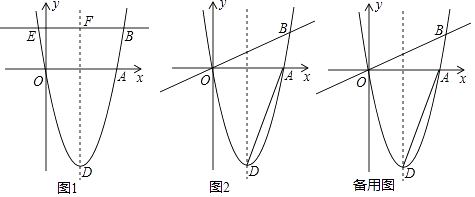
(1)当DF=4a时,求BE的长.
(2)如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上.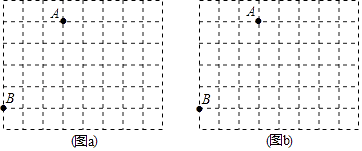
(1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;
(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形,且tan∠ABD=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
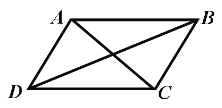
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com