练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知一次函数y=（m-2）x+m图象不经过第三象限，那么实数m的取值范围是0≤m＜2．

    分析 根据一次函数于与系数的关系得到m-2＜0且m≥0，然后写出两个不等式的公共解即可．

    解答 解：∵一次函数y=（m-2）x+m图象不经过第三象限，
    即图象经过第一、二、四象限或图象经过二、四象限和原点，
    ∴m-2＜0且m≥0，
    ∴0≤m＜2．
    故答案为0≤m＜2．

    点评 本题考查了一次函数图象与系数的关系：对于y=kx+b，当k＞0，b＞0?y=kx+b的图象在一、二、三象限；k＞0，b＜0?y=kx+b的图象在一、三、四象限；k＜0，b＞0?y=kx+b的图象在一、二、四象限；k＜0，b＜0?y=kx+b的图象在二、三、四象限．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图，已知∠A=ɑ，∠ACD 是△ABC 的外角，∠ABC 的平分线与∠ACD 的平分线相交于点 A1，得∠A1；若∠A1BC 的 平分线与∠A1CD 的平分线相交于点 A2，得∠A2…∠A2015BC 的平分线与∠A2015CD 的平分线相交于点 A2016，得∠A2016，则∠A2016=$\frac{α}{{2}^{2016}}$．（用含ɑ的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．计算：${36^{\frac{1}{2}}}×{49^{\frac{1}{2}}}$=42．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．对于平面直角坐标系中的点P（a，b），若点P′的坐标为（a+$\frac{b}{k}$，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”．
    例如：P（1，4）的“2属派生点”为P′（1+$\frac{4}{2}$，2×1+4），即P′（3，6）．
    （1）点P（-1，-2）的“2属派生点”P′的坐标为（-2，-4）；
    （2）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且△OPP′为等腰直角三角形，则求k的值；
    （3）如图，点A在函数y=-$\frac{4\sqrt{3}}{x}$（x＜0）的图象上，且点A是点B的“-$\sqrt{3}$属派生点”，问点B是否在直线y=$\sqrt{3}$x+2$\sqrt{3}$上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

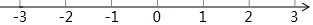    9．把75%，2的相反数，$-2\frac{1}{3}$，-（-3），-12各数所表示的点在数轴上分别用字母“A、B、C、D、E”标出来，再用“＜”把这些数连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．已知x满足2（x+3）2=32，则x等于-6或2．近似数 2.30×104精确到百位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，如果∠A：∠B：∠C=1：2：3，那么△ABC的形状是直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算：-9÷$\frac{1}{3}$=-27．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=$\frac{k}{x}$（x＞0）的图象与BC边交于点E．
    （1）当F为AB的中点时，求该反比例函数的解析式和点E的坐标．
    （2）设过（1）中的直线EF的解析式为y=ax+b，直接写出不等式ax+b＜$\frac{k}{x}$的解集．
    （3）当k为何值时，△AEF的面积最大，最大面积是多少？

    查看答案和解析>>

    同步练习册答案