
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B与y轴交于C,过C作x轴的平行线交抛物线于点D,过点D作x轴的垂线交x轴于E,点D的坐标为(2,3)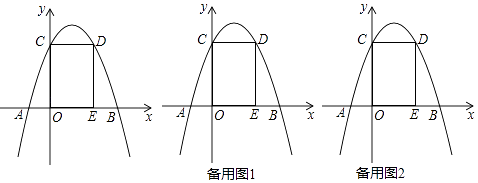
(1)求抛物线的解析式;
(2)点P为第一象限直线DE右侧抛物线上一点,连接AP交y轴于点F,连接PD、DF,设点P的横坐标为t,△PFD的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点P向下平移3个单位得到点Q,连接AQ、EQ,若∠AQE=45°,求点P的横坐标.
【答案】
(1)解:由题意D(2,3),C(0,3),
∵CD∥x轴,
∴C、D关于对称轴对称,
∴对称轴x=1,
∴﹣ ![]() =1,
=1,
∴b=2,c=3,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)解:如图1中,连接PC,作PH⊥AB于H.设P(t,﹣t2+2t+3).
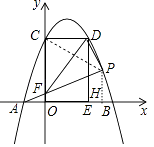
对于抛物线y=﹣x2+2x+3,令y=0,﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0)
∵OF∥PB,
∴ ![]() =
= ![]() ,
,
∴FO=(﹣t2+2t+3) ![]() =3﹣t,
=3﹣t,
∴CF=3﹣(3﹣t)=t,
S=S△PCF+S△PCD﹣S△CDF= ![]() tt+
tt+ ![]() ×2×[3﹣(﹣t2+2t+3)]﹣
×2×[3﹣(﹣t2+2t+3)]﹣ ![]() t2=
t2= ![]() t2﹣3t(2<t<3).
t2﹣3t(2<t<3).
(3)解:如图构造等腰直角三角形△AKE,使得AK=EK,∠AKE=90°,则易知K( ![]() ,﹣
,﹣ ![]() ),以K为圆心,AK为半径画⊙K.
),以K为圆心,AK为半径画⊙K.
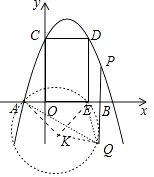
∵∠AQE=45°= ![]() ∠AKE,
∠AKE,
∴点Q在⊙K上,设P(m,﹣m2+2m+3),则Q(m,﹣m2+2m),
∵AK=QK,
∴(1+ ![]() )2+(
)2+( ![]() )2=(m﹣
)2=(m﹣ ![]() )2+(﹣m2+2m+
)2+(﹣m2+2m+ ![]() )2,
)2,
∴ ![]() +
+ ![]() =m2﹣m+
=m2﹣m+ ![]() +(﹣m2+2m)2+3(﹣m2+2m)+
+(﹣m2+2m)2+3(﹣m2+2m)+ ![]() ,
,
∴m2﹣m﹣2+m2(m﹣2)2﹣3m(m﹣2)=0,
∴(m﹣2)(m+1)+m2(m﹣2)2﹣3m(m﹣2)=0,
∴(m﹣2)[(m+1)+m3﹣2m2﹣3m]=0,
∴(m﹣2)[(m+1)+m(m+1)(m﹣3)]=0,
∴(m﹣2)(m+1)(m2
∴m=2或﹣1或 ![]() ,
,
∵点P为第一象限直线DE右侧抛物线上一点,
∴m= ![]() ,
,
∴满足条件的点P的横坐标为 ![]() .
.
【解析】(1)根据题意易求得点C的坐标,再用待定系数法求出抛物线的解析式。或根据点C、D是两对称点,求出对称轴,即可求出抛物线的解析式。
(2)观察函数图像,可知S△PFD=S△PCF+S△PCD﹣S△CDF,因此连接PC,作PH⊥AB于H.设P(t,﹣t2+2t+3),再用含t的代数式分别求出△PCF、△PCD、△CDF的面积,就可以求出S与t的函数关系式。
(3)抓住已知∠AQE=45°,添加辅助线,构造圆周角为45°的圆心角,构造等腰直角三角形△AKE,使得AK=EK,∠AKE=90°,以K为圆心,AK为半径画⊙K,易得到K点坐标,得出点Q在圆上,设出点P、点Q的坐标,根据AK=QK。列出方程,求解即可求出点P的横坐标。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水
(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请用尺规作图,将上述两种情况下的自来水厂厂址分别在图(1)(2)中标出,并保留作图痕迹。

查看答案和解析>>
科目:初中数学 来源: 题型:
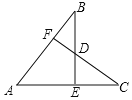
【题目】如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. ![]() B.
B. ![]() C. 点D在
C. 点D在![]() 的平分线上D. 点D是CF的中点
的平分线上D. 点D是CF的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】便民服装店的老板在株洲看到一种夏季衬衫,就用8000元购进若干件,以每件58元的价格出售,很快售完,又用17600元购进同种衬衫,数量是第一次的2倍每件进价比第一次多了4元,服装店仍按每件58元出售,全部售完,问该服装店两次一共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
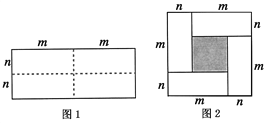
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com