
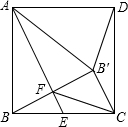
 在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①根据轴对称图形的性质,可知△ABF与△AB′F关于AE对称,即得AB′=AD;
②连接EB′,根据E为BC的中点和线段垂直平分线的性质,求出∠BB′C为直角三角形;
③假设∠ADB′=75°成立,则可计算出∠AB′B=60°,推知△ABB′为等边三角形,B′B=AB=BC,与B′B<BC矛盾;
④根据直角三角形的性质即可得到结论;
⑤根据相似三角形的判定和性质即可得到结论.
解答 解:①∵点B′与点B关于AE对称,
∴△ABF与△AB′F关于AE对称,
∴AB=AB′,
∵AB=AD,
∴AB′=AD.故①正确;
②如图,连接EB′.
则BE=B′E=EC,
∠FBE=∠FB′E,
∠EB′C=∠ECB′.
则∠FB′E+∠EB′C=∠FBE+∠ECB′=90°,
即△BB′C为直角三角形.
∵FE为△BCB′的中位线,
∴B′C=2FE,
∵△B′EF∽△AB′F,
∴$\frac{FE}{FB′}$=$\frac{EB′}{AB′}$,
即$\frac{FE}{FB′}$=$\frac{EB}{AB}$=$\frac{1}{2}$,
故FB′=2FE.
∴B′C=FB′.
∴△FCB′为等腰直角三角形.
故②正确.
③设∠ABB′=∠AB′B=x度,
∠AB′D=∠ADB′=y度,
则在四边形ABB′D中,2x+2y+90°=360°,
即x+y=135度.
又∵∠FB′C=90°,
∴∠DB′C=360°-135°-90°=135°.
故③正确.
④∵∠BB′C=90°,
∴BB′<BC,
故④错误;
⑤∵∠ABE=90°,BF⊥AE,
∴∠ABE=∠AFB=90°,
∵∠BAF=∠BAF,
∴△ABF∽△AEB,
∴$\frac{AB}{AE}$=$\frac{AF}{AB}$,
∴AB2=AE•AF;
故⑤正确,
故选:C.
点评 此题考查了正方形的性质、等腰直角三角形的判定和性质,等边三角形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com