
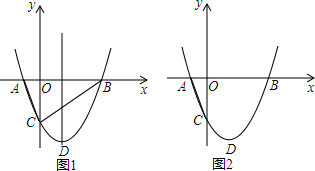
分析 (1)把点A的坐标代入函数解析式来求b的值;然后把函数解析式转化为顶点式,即可得到点D的坐标;
(2)由两点间的距离公式分别求出AC,BC,AB的长,再根据勾股定理即可判断出△ABC的形状;
(3)根据抛物线的对称性可知AM=BM.所以AM+CM=BM+CM≥BC=2$\sqrt{5}$;
(4)过点P作y轴的平行线交BC于F.利用待定系数法求得直线BC的解析式,可求得点F的坐标,设P点的横坐标为m,可得点P的纵坐标,继而可得线段PF的长,然后利用面积和即S△PBC=S△CPF+S△BPF=$\frac{1}{2}$PF×BO,即可求出.
解答 解:(1)把A(-1,0)代入$y=\frac{1}{2}{x^2}+bx-2$得到:0=$\frac{1}{2}$×(-1)2-b-2,
解得b=-$\frac{3}{2}$,
则该抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
又∵y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
∴顶点D的坐标是($\frac{3}{2}$,-$\frac{25}{8}$);
(2)由(1)知,该抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.则C(0,-2).
又∵y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$(x+1)(x-4),
∴A(-1,0),B(4,0),
∴AC=$\sqrt{5}$,BC=2$\sqrt{5}$,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形; (3)由(2)知,B(4,0),C(0,-2),
(3)由(2)知,B(4,0),C(0,-2),
由抛物线的性质可知:点A和B关于对称轴对称,如答图1所示:
∴AM=BM,
∴AM+CM=BM+CM≥BC=2$\sqrt{5}$.
∴CM+AM的最小值是2$\sqrt{5}$;
(4)如答图2,过点P作y轴的平行线交BC于F.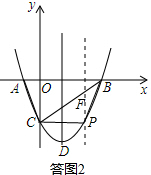 设直线BC的解析式为y=kx-2(k≠0).
设直线BC的解析式为y=kx-2(k≠0).
把B(4,0)代入,得
0=4k-2,
解得k=$\frac{1}{2}$.
故直线BC的解析式为:y=$\frac{1}{2}$x-2.
故设P(m,$\frac{1}{2}$m2-$\frac{3}{2}$m-2),则F(m,$\frac{1}{2}$m-2),
∴S△PBC=$\frac{1}{2}$PF•OB=$\frac{1}{2}$×($\frac{1}{2}$m-2-$\frac{1}{2}$m2+$\frac{3}{2}$m+2)×4=-(m-2)2+4,即S△PBC=-(m-2)2+4,
∴当m=2时,△PBC面积的最大值是4.
点评 此题考查了二次函数综合应用,要注意数形结合,认真分析,仔细识图.注意待定系数法求函数的解析式,注意函数交点坐标的求法,三角形面积的求法.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
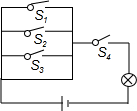 如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )
如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
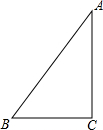 某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)
某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com