

���� ��1���ڵ���������ABE����á�EAB�Ķ������ڵ���������EAD����á�EAD�Ķ��������ɵõ���ADF�Ķ�����
��2�������PAB=�������ݵ��������ε����ʣ���á�AEB�͡�AED�Ķ��������ݡ�BEF=��AEB-��AED���ɵõ���BEFΪ��ֵ��
��3�������PAB=�£����ݵ��������ε����ʣ���á�AEB�͡�AED�Ķ��������ݡ�BEF=��AED+��AEB���ɵõ���BEFΪ��ֵ��
��� �⣺��1���ߵ�B����ֱ��AP�ĶԳƵ�ΪE����PAB=20�㣬
��AE=AB����EAB=40�㣬
��������ABCD�У�AB=AD����BAD=90�㣬
��AE=AD����EAD=130�㣬
�����������AED�У���ADF=25�㣻
��2����ͼ1�����PAB=�������EAB=2����
���AEB=90��-������AED=$\frac{180��-��90��+2����}{2}$=45��-����
���BEF=��AEB-��AED=90��-��-��45��-����=45�㣻
��3����ͼ��ʾ����BEF�Ķ������ᷢ���仯����Ϊ45��
���PAB=�£�
ͬ���ɵã���EAB=2�£���AEB=90��-�£�
���EAD=360��-90��-2��=270��-2�£�
�����������ADE�У���AED=$\frac{180��-��270��-2�£�}{2}$=��-45�㣬
���BEF=��AED+��AEB=��-45��+90��-��=45�㣨��ֵ����
���� ������Ҫ�����������ε������Լ����������ε����ʣ��������Ĺؼ��Ǹ��ݵ��������ε����������ǻǵĶ������ٸ��ݽǵĺͲ��ϵ�ó����ۣ�����ʱע�⣬�������ͼ�ι���ijֱ�߶Գƣ���ô�Գ������κ�һ�Զ�Ӧ�������߶εĴ�ֱƽ���ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
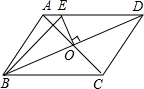 ��ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����AD��CD������O��OE��BD����AD�ڵ�E�������ABE���ܳ�Ϊ4����ôƽ���ı���ABCD���ܳ���8��
��ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����AD��CD������O��OE��BD����AD�ڵ�E�������ABE���ܳ�Ϊ4����ôƽ���ı���ABCD���ܳ���8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ��������OABC�Ķ���O������ԭ�㣬����C��A�ֱ���x�ᡢy����������ϣ��߳�Ϊ4����N�DZ�BC���е㣬��D��OC���е㣮
��ͼ����ƽ��ֱ������ϵ��������OABC�Ķ���O������ԭ�㣬����C��A�ֱ���x�ᡢy����������ϣ��߳�Ϊ4����N�DZ�BC���е㣬��D��OC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������y=$\frac{m}{n}$��m��0����ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D��0��4������A������Ϊ��n��6������tan��ACO=2��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������y=$\frac{m}{n}$��m��0����ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D��0��4������A������Ϊ��n��6������tan��ACO=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com