
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=8,点P从点A出发,沿折线AC-CB以每秒2个单位长度的速度向终点B运动,当点P不与点A,B重合时,在边AB上取一点Q,满足∠PQA=2∠B,过点Q作QM⊥PQ,交边BC于点M,以PQ,QM为边作矩形PQMN,设点P的运动时间为t秒.

(1)直接写出线段PQ的长(用含t的代数式表示);
(2)当矩形PQMN为正方形时,求t的值;
(3)设矩形PQMN与△ABC重叠部分的面积为S,求S与t之间的函数关系式.
【答案】(1)当0<t≤2时,PO= ![]() t,当2<t<6时,PQ=
t,当2<t<6时,PQ= ![]() t+3
t+3 ![]() ;(2)t=
;(2)t= ![]() ;(3)S=
;(3)S=![]() -
- ![]() t+
t+ ![]()
【解析】
(1)利用行程问题的等量关系用含t的代数式表示出线段AP的长,利用勾股定理求出AB的长,然后分两种情况解答:
①当0<t≤2时,作QH⊥AC,可得QH∥BC,则∠AQH=∠B,已知∠PQA=2∠B,故可得∠AQH=∠PQH,从而可得△AQH≌△PAH,利用全等三角形对应边相等可得PQ=AQ;然后易证△AQH∽△ABC,利用相似三角形的对应边成比例列出比例式即可求出线段AQ,而PQ=AQ,故而可求;
②当2<t<6时,作QG⊥BC,可得PQ=QB,利用△BQG∽△BAC对应边成比例求解,解法同①;
(2)分两种情况求解:①当0<t≤2时,作QD⊥AC,QE⊥BC,利用正方形的性质易证△DQP≌△EQM,则DQ=EQ,即t+2t=4,解得值即可;②当2<t<6时,PQ=QB>QM,则可判断PQMN不可能是正方形;
(3)分0<t≤2和2<t<6两种情况,用割补法求出重合部分的面积即可;
(1)当0<t≤2时,作QH⊥AC,可得QH∥BC,则∠AQH=∠B,已知∠PQA=2∠B,故可得∠AQH=∠PQH,从而可得△AQH≌△PAH,利用全等三角形对应边相等可得PQ=AQ;然后易证△AQH∽△ABC,利用相似三角形的对应边成比例列出比例式即可求出线段AQ,而PQ=AQ,故而可求PO= ![]() t;当2<t<6时,作QG⊥BC,可得PQ=QB,利用△BQG∽△BAC对应边成比例,得到PQ=
t;当2<t<6时,作QG⊥BC,可得PQ=QB,利用△BQG∽△BAC对应边成比例,得到PQ= ![]() (6-t)=
(6-t)= ![]() t+3
t+3 ![]() .
.
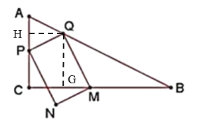
(2)解:当2<t<6时,PQ=QB>QM,此时矩形PQMN不可是正方形.
当0<t≤2时,
如图,过点Q分别作AC,BC的垂线,垂足为D,E.
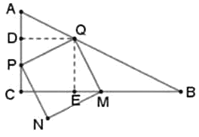
∵∠PQM=∠DQE=90°,
∴∠DQP=∠EQM,
又∠PDQ=∠MEQ=90°,PQ=MQ,
∴△DQP≌△EQM(AAS),
∴DQ=EQ
∴t+2t=4,解得t= ![]()
即,当t= ![]() 时,矩形PQMN为正方形
时,矩形PQMN为正方形
(3)当0<t≤2时,S=PQ·QM- ![]() =
= ![]() t·
t· ![]() (4-t)-
(4-t)- ![]() =
= ![]() +10t;当2<t<6时,S=
+10t;当2<t<6时,S= ![]() =
= ![]() =
= ![]() -
- ![]() t+
t+ ![]() .
.


科目:初中数学 来源: 题型:
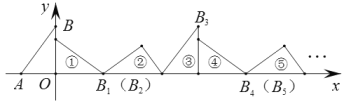
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
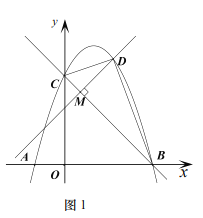
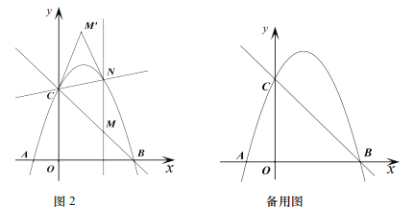
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,原价每千克25元,连续两次涨价后每千克水果现在的价格为36元.
(1)若每次涨价的百分率相同.求每次涨价的百分率;
(2)若进价不变,按现价售出,每千克可获利15元,但该水果出现滞销,商场决定降价m元出售,同时把降价的幅度m控制在![]() 的范围,经市场调查发现,每天销售量
的范围,经市场调查发现,每天销售量![]() (千克)与降价的幅度m(元)成正比例,且当
(千克)与降价的幅度m(元)成正比例,且当![]() 时,
时,![]() . 求
. 求![]() 与 m的函数解析式;
与 m的函数解析式;
(3)在(2)的条件下,若商场每天销售该水果盈利![]() 元,为确保每天盈利
元,为确保每天盈利![]() 最大,该水果每千克应降价多少元?
最大,该水果每千克应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲,乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.求甲,乙两种物品的单价各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
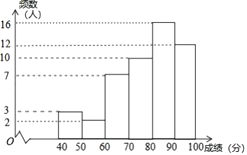
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 的对称轴是直线
的对称轴是直线![]() 与
与![]() 轴的交点为点
轴的交点为点![]() 且经过点
且经过点![]() 两点.
两点.
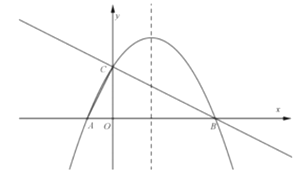
(1)求抛物线的解析式;
(2)点![]() 为抛物线对称轴上一动点,当
为抛物线对称轴上一动点,当![]() 的值最小时,请你求出点
的值最小时,请你求出点![]() 的坐标;
的坐标;
(3)抛物线上是否存在点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() 使得以点
使得以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com