
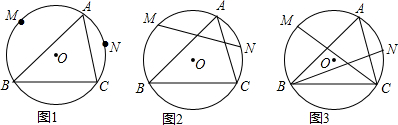
分析 (1)①连接AM、AN,利用等弧所对的圆周角相等结合三角形的外角的性质,可证得结论;②由①可得△EMA∽△FAN,利用相似三角形的性质结合已知条件可得到AE2+AF2=EF2,可求得∠A;
(2)由条件可得到$\widehat{BC}$=$\widehat{MAN}$=$\widehat{BM}$+$\widehat{CN}$=$\frac{1}{3}$⊙O,可求得∠A的度数,
(3)①连接CM、BN,相交于一点Q,连接AQ并延长交⊙O于点P,根据三角形角平分线的性质可知点P即为所求;②连接OA、OB、OM,则AB⊥OM,可用AB表示出四边形OAMB的面积,同理可表示出四边形OBPC、四边形OCNA的面积,可求得六边形AMBPCN的面积.
解答 解:
(1)①证明:
如图1,连接AM、AN,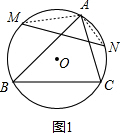
∵点M是$\widehat{AB}$的中点,点N是$\widehat{AC}$的中点,
∴$\widehat{AM}$=$\widehat{BM}$,$\widehat{AN}$=$\widehat{CN}$,
∴∠EMA=∠FAN,∠EAM=∠FNA,
∴∠AEF=∠EMA+∠EAM=∠FAN+∠FNA=∠AFE,
∴AE=AF;
②由①可知△EMA∽△FA,
∴$\frac{AE}{NF}$=$\frac{ME}{AF}$,
∴AE2=AF2=ME•MF,
又2ME•MF=EF2,
∴AE2+AF2=EF2,
∴∠BAC=90°;
(2)∵CM=BN,
∴有$\widehat{MBC}$=$\widehat{BCN}$或$\widehat{MBC}$=$\widehat{BMAN}$,
①当$\widehat{MBC}$=$\widehat{BCN}$时,则有$\widehat{MB}$=或$\widehat{CN}$,$\widehat{AMB}$=$\widehat{ANC}$,
∴AB=AC,这与AB≠AC矛盾;
②当$\widehat{MBC}$=$\widehat{BMAN}$时,则有$\widehat{BC}$=$\widehat{MAN}$,
又$\widehat{MAN}$=$\widehat{AM}$+$\widehat{AN}$=$\widehat{BM}$+$\widehat{CN}$,
∴$\widehat{BC}$=$\widehat{MAN}$=$\widehat{BM}$+$\widehat{CN}$=$\frac{1}{3}$⊙O,
∴∠BOC=120°,
∴∠BAC=60°;
(3)①如图2,连接CM、BN交于点Q,连接AQ并延长,交⊙O于点P,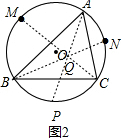
∵点M是$\widehat{AB}$的中点,点N是$\widehat{AC}$的中点,
∴CM、BN分别平分∠BCA和∠CBA,
∴AP平分∠BAC,
∴∠BPA=∠CPA,
∴$\widehat{BP}$=$\widehat{CP}$,
即P为$\widehat{BC}$的中点;
②连接OA、OB、MO,如图3,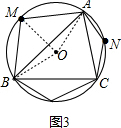
∵点M是$\widehat{AB}$的中点,
∴OM⊥AB,且OM=1,
∴S四边形OAMB=$\frac{1}{2}$OM•AB=$\frac{1}{2}$AB,同理可得S四边形OBPC=$\frac{1}{2}$BC,S四边形OCNA=$\frac{1}{2}$AC,
∴S六边形AMBPCN=S四边形OAMB+S四边形OBPC+S四边形OCNA=$\frac{1}{2}$AB+$\frac{1}{2}$BC+$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC+CA)=$\frac{1}{2}$×4=2.
点评 本题为圆的综合应用,涉及知识点有圆的性质、相似三角形的判定和性质、三角形角平分线的性质、圆周角定理、垂径定理及转化思想等.在(2)中求出$\widehat{BC}$是$\frac{1}{3}$⊙O是解题的关键,在(3)②中利用垂径定理求得四边形OAMB的面积,把六边形的面积化为三个四边形的面积是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
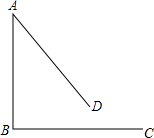 已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.
已知:AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
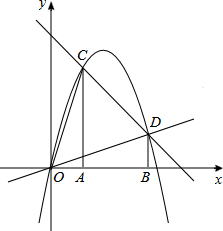 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com