
分析 (1)画出树形图,得到所有可能结果,找到2个球颜色不同的数目,即可求出其概率.
(2)根据在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,由白球的频率,即可求出x的值.
解答 解:
(1)树状图如下所示:
由树形图可知所有可能情况共12种,其中2个球颜色不同的数目有6种,
所以2个球颜色不同的概率=$\frac{6}{12}$=$\frac{1}{2}$;
(2)由题意可得:$\frac{3+x}{4+x}$=0.95,
解得:x=16,
经检验x=16是原方程的解,
所有x的值为16.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.同时本题还考查利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
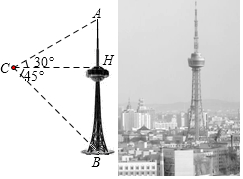 吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)
吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC是⊙O的直径,∠ACB=90°,CA=CB,连接BO交⊙O于点D,连接AD,则tan∠ADO的值为( )
如图,AC是⊙O的直径,∠ACB=90°,CA=CB,连接BO交⊙O于点D,连接AD,则tan∠ADO的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{2}{3}$ | C. | 3-$\sqrt{5}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com