
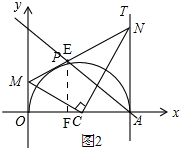
 如图,已知A(4,0),过A作x轴的垂线AT,以OA为直径作半圆,圆心为C,M是y轴正半轴上一动点(与O点不重合),过M作半圆的切线MN交直线AT于N,切点为P,连结CN、CM.
如图,已知A(4,0),过A作x轴的垂线AT,以OA为直径作半圆,圆心为C,M是y轴正半轴上一动点(与O点不重合),过M作半圆的切线MN交直线AT于N,切点为P,连结CN、CM.分析 (1)先判断出Rt△ACN≌Rt△PCN,得出∠PCN=∠ACN=$\frac{1}{2}$∠ACP,同理:∠OCM=∠PCM=$\frac{1}{2}$∠OCP,从而得出结论;
(2)先确定出C(2,0),M(0,m),再判断出△OCM∽△ANC,确定出AN=$\frac{4}{m}$,N(4,$\frac{4}{m}$),用待定系数法即可;
(3)先求出直线MN解析式为y=$\frac{3}{4}$x+1,再求出梯形OANM的面积,设出点E坐标,用面积公式即可.
解答 解:(1) 连接OP,
连接OP,
∵A作x轴的垂线AT,以OA为直径作半圆,
∴∠CAN=90°,
∵MN是⊙C的切线,
∴∠OPC=90°,
在Rt△ACN和△RtPCN中,$\left\{\begin{array}{l}{CP=CA}\\{CN=CN}\end{array}\right.$,
∴Rt△ACN≌Rt△PCN,
∴∠PCN=∠ACN=$\frac{1}{2}$∠ACP,
同理:∠OCM=∠PCM=$\frac{1}{2}$∠OCP,
∵∠ACP+∠OCP=180°,
∴∠MCP∠+∠NCP=90°,
∴∠MCN=90°,
(2)∵点A(4,0),且AB为直径圆C,
∴C(2,0),
∵OM=m,且点M在y轴正半轴上,
∴M(0,m),
由(1)得,∠OCM+∠ACN=90°
∵∠ACN+∠ANC=90°,
∴∠OCM=∠ANC,
∵∠COM=∠CAN=90°,
∴△OCM∽△ANC,
∴$\frac{OC}{AN}=\frac{OM}{AC}$,
∴$\frac{2}{AN}=\frac{m}{2}$,
∴AN=$\frac{4}{m}$,
∴N(4,$\frac{4}{m}$),
设抛物线解析式为y=a(x-2)2,
∵点M,N在抛物线上,
∴$\left\{\begin{array}{l}{\frac{4}{m}=a(4-2)^{2}}\\{m=a(0-2)^{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=2}\\{a=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=-2}\\{a=-\frac{1}{2}}\end{array}\right.$(舍),
∴抛物线解析式为y=$\frac{1}{2}$(x-2)2,m=2,
(3)∵OM=1
由(2)有,AN=4,
∴S梯形OANM=$\frac{1}{2}$(OM+AN)×OA=$\frac{1}{2}$(1+4)×4=10,
∵M(0,1),N(4,4),
∴直线MN解析式为y=$\frac{3}{4}$x+1,
∵过A点且平分梯形OMNA面积的直线与MN相交于E,过点E作EF⊥OA,
设E(n,$\frac{3}{4}$n+1),
∴EF=$\frac{3}{4}$n+1,AF=4-n
S四边形OAEN
= S梯形OFEM+S△AEF=$\frac{1}{2}$(OM+EF)×OF+$\frac{1}{2}$AF×EF
S梯形OFEM+S△AEF=$\frac{1}{2}$(OM+EF)×OF+$\frac{1}{2}$AF×EF
=$\frac{1}{2}$(1+$\frac{3}{4}$n+1)×n+$\frac{1}{2}$×(4-n)×($\frac{3}{4}$n+1)
=$\frac{1}{2}$S梯形OANM
=5,
∴n=$\frac{3}{2}$,
∴N($\frac{3}{2}$,$\frac{17}{8}$),
设直线AE的解析式为y=kx+b,且A(4,0),
∴$\left\{\begin{array}{l}{4k+b=0}\\{\frac{3}{2}k+b=\frac{17}{8}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{17}{20}}\\{b=\frac{17}{5}}\end{array}\right.$
∴过A点且平分梯形OMNA面积的直线解析式y=-$\frac{17}{20}$k+$\frac{17}{5}$.
点评 此题是二次函数综合题,主要考查了切线的性质,全等三角形的性质和判定,相似三角形的判定和性质,待定系数法,解本题的关键是用分割法求出四边形OAEM的面积.


科目:初中数学 来源: 题型:填空题
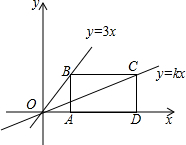 如图,点B、C分别在两条直线y=3x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是长方形,且BC=2AB,则k的值为$\frac{3}{7}$.
如图,点B、C分别在两条直线y=3x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是长方形,且BC=2AB,则k的值为$\frac{3}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1的平方根是1 | |
| B. | 6是36的算术平方根 | |
| C. | 同一平面内的三条直线满足a⊥b,b⊥c,则a⊥c | |
| D. | 两直线被第三条直线所截,内错角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=$\frac{x}{2}$ | C. | y=$\frac{2}{x}$ | D. | y=$\frac{x+1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com