
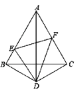
【题目】如图所示,D是等边三角形ABC外一点,![]() ,点E,F分别在
,点E,F分别在![]() 上
上
(1)求证:AD是BC的垂直平分线
(2)若ED平分![]() ,求证FD平分
,求证FD平分![]() .
.
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
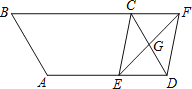
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-4x+c,函数值y与自变量x之间的部分对应值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
(1)求这个二次函数的关系式.
(2)直接写出m、n、k之间的大小关系.(用“>”连接)
(3)若点P在这个二次函数的图象上,且点P到x轴的距离为1,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
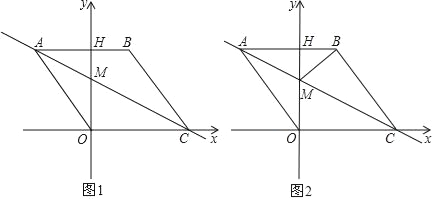
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() .
.
(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中![]() 与⊙
与⊙![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
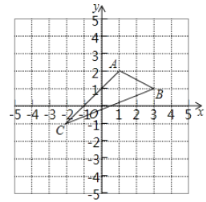
【题目】如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.
(2)写出点A1,B1,C1的坐标(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.
(1)求甲、乙两种商品的进价各是多少元?
(2)该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川省雅安市芦山县(北纬30.3度,东经103.0度)2013年4月20日8点02分发生7.0级地震,震源深度13千米.截至4月25日18时,地震遇难人数升至196人,失踪21人,13484人受伤,累计造成231余万人受灾.一方有难,八方支援”.雅安地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援雅安.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com