(1)证明:在△ABM和△BCN中,
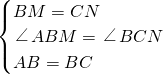
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60;
(2)解:①是;②是;③否;
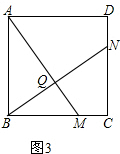
②的证明:如图,
在△ACM和△BAN中,

,
∴△ACM≌△BAN(SAS),
∴∠AMC=∠BNA,
∴∠NQA=∠NBC+∠BMQ=∠NBC+∠BNA=180°-60°=120°,
∴∠BQM=60°;
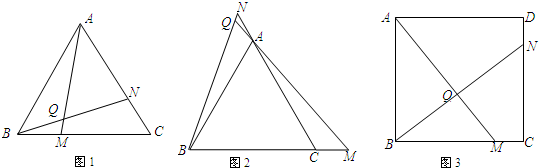
③的证明:如图,
在Rt△ABM和Rt△BCN中,

,
∴Rt△ABM≌Rt△BCN(SAS),
∴∠AMB=∠BNC.
又∵∠NBM+∠BNC=90°,
∴∠QBM+∠QMB=90°,
∴∠BQM=90°,即∠BQM≠60°.
分析:(1)根据等边三角形性质得出AB=AC,∠ABC=∠C=60°,根据SAS证△ABM≌△BCN,推出∠NBC=∠BAM,求出∠BAM+∠ABN=60°即可;
(2)①根据∠BQM=60°和∠ABC=60°求出∠BAM=∠CBN,推出△BCN≌△ABM即可;
②同样还是根据条件判定△ACM≌△BAN,得到∠AMC=∠BNA,所以∠NQA=∠NBC+∠BMQ=∠NBC+∠BNA=180°-60°=120°,即∠BQM=60°;
③同上,证明Rt△ABM≌Rt△BCN,得到∠AMB=∠BNC,所以,∠QBM+∠QMB=90°,∠BQM=90°,即∠BQM≠60°.
点评:主要考查了等边三角形的性质和全等三角形的判定及性质;判定两个三角形全等的一般方法有:SSS、SAS、ASA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

 ,
, ,
, 在Rt△ABM和Rt△BCN中,
在Rt△ABM和Rt△BCN中, ,
,

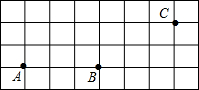 如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等.
如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等. 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中: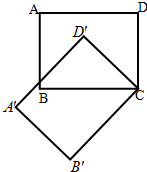 25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题: