
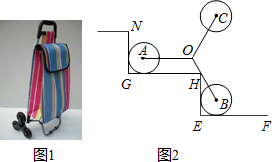
 如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$.
如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$. 分析 如图,作OK⊥GH,BT⊥HE垂足分别为K、T,设圆的半径都是r,分别求出OH、HB即可解决问题.
解答 解:如图,作OK⊥GH,BT⊥HE垂足分别为K、T,设圆的半径都是r,
在Rt△OKH中,∵∠OKH=90°,OK=r,∠OHK=180°-∠AOB=60°,
∴cos60°=$\frac{OK}{OH}$,
∴OH=$\frac{2\sqrt{3}}{3}$r,
在Rt△HTB中,∵∠HTB=90°,BT=r,∠THB=30°,
∴BH=2BT=2r,
∴$\frac{BH}{OH}$=$\frac{2r}{\frac{2\sqrt{3}}{3}}$=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查切线的性质、直角三角形30度角性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3中能判断直线l1∥l2的有( )
如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3中能判断直线l1∥l2的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在长方形桌面CDEF的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,如果∠1=40°,那么∠AFE=10°.
如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在长方形桌面CDEF的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,如果∠1=40°,那么∠AFE=10°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com