
分析 (1)根据平方差公式求出即可;
(2)先根据完全平方公式变形,再代入求出即可;
(3)先根据平方差公式和完全平方公式展开,再合并同类项即可.
解答 解:(1)(-5x+2y)(-2y-5x)
=(-5x)2-(2y)2
=25x2-4y2;
(2)∵x+$\frac{1}{x}$=-8,
∴x2+$\frac{1}{{x}^{2}}$
=(x+$\frac{1}{x}$)2-2•x•$\frac{1}{x}$
=(-8)2-2
=62;
(3)4(x+2)2-(-2x+3)(-2x-3)
=(4x2+16x+16)-(4x2-9)
=4x2+16x+16-4x2+9
=16x+25.
点评 本题考查了整式的混合运算,平方差公式,完全平方公式的应用,能灵活运用知识点进行化简是解此题的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
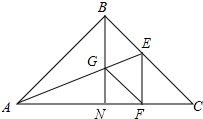 如图,在△ABC中,BA=BC,∠ABC=90°,BN平分∠ABC,AE平分∠BAC,AE交BN于G,EF⊥AC于F,连接GF.①△AEB≌△AEF;②∠EFG=∠AFG;③图中有3对全等三角形;④EF=GF;⑤S△AEF=2S△AGN.上述结论正确的序号有①②④⑤.
如图,在△ABC中,BA=BC,∠ABC=90°,BN平分∠ABC,AE平分∠BAC,AE交BN于G,EF⊥AC于F,连接GF.①△AEB≌△AEF;②∠EFG=∠AFG;③图中有3对全等三角形;④EF=GF;⑤S△AEF=2S△AGN.上述结论正确的序号有①②④⑤.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com