【题目】 正方形ABCD与正五边形EFGHM的边长相等，初始如图所示，将正方形绕点F顺时针旋转使得BC与FG重合，再将正方形绕点G顺时针旋转使得CD与GH重合…按这样的方式将正方形依次绕点H、M、E旋转后，正方形中与EF重合的是（ ）
A. ABB. BCC. CDD. DA
寒假学与练系列答案科目：初中数学 来源： 题型：
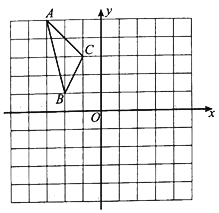
【题目】如图，在平面直角坐标系中，已知
的三个顶点的坐标分别为
，
，
．
（1）若
经过平移后得到
，已知点
的坐标为
，写出顶点
，
的坐标；
（2）若和
关于原点
成中心对称图形，写出各顶点的坐标；
（3）将绕着点O按顺时针方向旋转
得到
，写出的各顶点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF.
（1）求证AE＝BF；
（2）若正方形的边长是5，BE＝2，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若三个非零实数
，
，
满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数，，构成“和谐三组数”.
（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；
（2）若
，
，
三点均在函数
（
为常数，
）的图象上，且这三点的纵坐标
，
，
构成“和谐三组数”，求实数
的值；
（3）若直线
与轴交于点
，与抛物线
交于
，
两点.
①求证：
，
，
三点的横坐标
，
，
构成“和谐三组数”；
②若
，
，求点
与原点
的距离
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
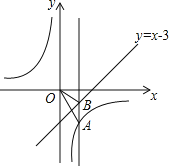
【题目】如图，已知点A、P在反比例函数y=
（k＜0）的图象上，点B、Q在直线y=x-3的图象上，点B的纵坐标为-1，AB⊥x轴，且S△OAB=4，若P、Q两点关于y轴对称，设点P的坐标为（m，n）．
（1）求点A的坐标和k的值；
（2）求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“六一”儿童节那天，小强去商店买东西，看见每盒饼干的标价是整数，于是小强拿出10元钱递给商店的阿姨，下面是他俩的对话：小强：“阿姨，我有10元钱，想买一盒饼干和一袋牛奶．”阿姨：“小朋友，本来你用10元钱买一盒饼干是有钱多的，但要再买一袋牛奶钱就不够了．不过今天是儿童节，饼干打九折，两样东西请你拿好，找你8角钱．”如果每盒饼干和每袋牛奶的标价分别设为x元，y元，请你根据以上信息：
（1）请你求出x与y之间的关系式；（用含x的式子表示y）
（2）请你根据上述条件，求出每盒饼干和每袋牛奶的标价．
查看答案和解析>>
科目：初中数学 来源： 题型：
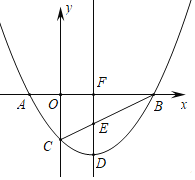
【题目】已知：如图，抛物线
与x轴交于A、B两点，与y轴交于C点，且
、
，点D是第四象限的抛物线上的一个动点，过点D作直线
轴，垂足为点F，交线段BC于点E
求抛物线的解析式及点A的坐标；
当
时，求点D的坐标；
在y轴上是否存在P点，使得
是以AC为腰的等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等腰直角三角形，∠ACB=90°，点E、F分别是边BC、AC的中点，P是AB上一点，以PF为一直角边作等腰直角三角形PFQ，且∠FPQ=90°，若AB=10，PB=1，则QE的值为（ ）
A. 3 B. 3
C. 4 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系 xOy 中，已知正比例函数 y1＝﹣2x 的图象与反比例函数 y2＝
的图象交于 A（﹣1，a），B 两点．
(1)求出反比例函数的解析式及点 B 的坐标；
(2)观察图象，请直接写出满足 y≤2 的取值范围；
(3)点 P 是第四象限内反比例函数的图象上一点，若△POB 的面积为 1，请直接写出点 P的横坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
