
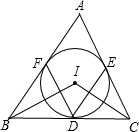
 ∠ABC,∠ICB=
∠ABC,∠ICB= ∠ACB,
∠ACB, (∠ABC+∠ACB),
(∠ABC+∠ACB),
 ∠EIF=70°,
∠EIF=70°, (∠ABC+∠ACB),
(∠ABC+∠ACB), (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A,
∠A, (180°-2β),
(180°-2β), (∠ABC+∠ACB),求出∠ABC+∠ACB的度数,求出∠IBC+∠ICB即可;连接IF、IE,求出∠FIE,即可求出∠FDE;
(∠ABC+∠ACB),求出∠ABC+∠ACB的度数,求出∠IBC+∠ICB即可;连接IF、IE,求出∠FIE,即可求出∠FDE; ∠A,代入即可求出答案.
∠A,代入即可求出答案.

科目:初中数学 来源: 题型:
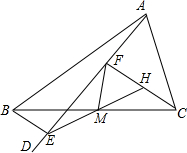 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )| A、BM=CM | ||
B、FM=
| ||
| C、CF⊥AD | ||
| D、FM⊥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( )
9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是
如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是| β+γ |
| 2 |
| β+γ |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com