
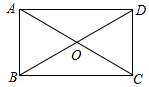
 如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8.
如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8.  挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
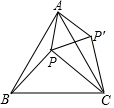 如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)
如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
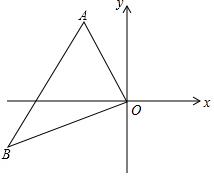 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )| A. | (-3,-1) | B. | (-1,2) | C. | (-9,1)或(9,-1) | D. | (-3,-1)或(3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.979×107元 | B. | 1.979×108元 | C. | 1.979×109元 | D. | 1.979×1010元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com