

���� ��1����ͼ1�У�����AO��BO��ֻҪ֤����AOC�ա�BOC�������õ������������ߺ�һ���ɽ�����⣮
��2����ͼ2�У��ӳ�BM����AE�ཻ�ڵ�F��ֻҪ֤����BME=2��BAE����GOC=��BAE���ɣ�
��3����ͼ3�У��ӳ�EG����O��K������OB��OE����OQ��BE��Q����EL��BM��L������֤��AN=KE������Rt��MEL�У����EL������Rt��BEL�У����BE�������Rt��BOQ�У����OB���ɣ�
��� ֤������1����ͼ1�У�����AO��BO��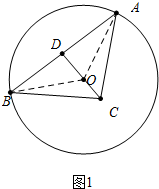
�ڡ�AOC�͡�BOC��
$\left\{\begin{array}{l}{CA=CB}\\{CO=CO}\\{OA=OB}\end{array}\right.$��
���AOC�ա�BOC
���ACO=��BCO
��AD=BD
֤������2����ͼ2�У��ӳ�BM����AE�ཻ�ڵ�F��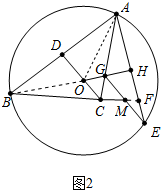
��OH��AE��
��AH=EH����GA=GE
���GAE=��E=�����֡�OA=OB��
���BAC=��B=��
�ߡ�BFE=��B+��BAE
���BME=��BFE+��E=2��+2��=2��BAE��
�֡�OA=OB��AD=DB��
��OD��AB��
�ߡ�GOC+��DOH=180�㣬��BAE+��DOH=180�㣬
���GOC=��BAE��
���BME=2��GOC
�⣺��3����ͼ3�У��ӳ�EG����O��K������OB��OE����OQ��BE��Q����EL��BM��L��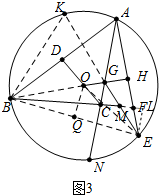
�ߡ�GOC=��BAE=60�㣬��BME=120�㣬AG=GE��
���GAE=��GEA��
��$\widehat{AK}$=$\widehat{EN}$��
��$\widehat{KE}$=$\widehat{AN}$
��EK=GN=8��
�֡�ME=2��
��KM=6����BE=��BE��
���K=��BAE=60�㣬
�ߡ�KMB=180��-��BME=60�㣬
���K=��KMB=60�㣬
���KBM�ǵȱ�������
��BK=BM=KM=6��
��Rt��EML�У��ߡ�ELM=90�㣬��EML=60�㣬EM=2��
��ME=1��EL=$\sqrt{3}$
��BE=$\sqrt{B{L}^{2}+E{L}^{2}}$=2$\sqrt{13}$
Rt��OBQ�У���BOQ=60�㣬BQ=$\sqrt{13}$��
���OBQ=30�㣬
��OB=2OQ����OQ=m����OB=2m��
�ࣨ2m��2=m2+��$\sqrt{13}$��2��
��m=��$\frac{\sqrt{39}}{3}$��
��m��0��
��m=$\frac{\sqrt{39}}{3}$
��OQ�T2m=$\frac{{2\sqrt{39}}}{3}$��
���� ���⿼��Բ�ۺ��⡢ȫ�������ε��ж������ʡ����ɶ������ȱ������ε��ж������ʡ���ֱ��������30�Ƚ����ʵ�֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ��ѧ���������ø����ߣ�����ֱ�������Σ������п�ѹ���⣮


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��I�ǡ�ABC�����ģ���BAC��ƽ���ߺ͡�ABC�����Բ�ཻ�ڵ�D��BD��ID�����Ϊʲô��
��ͼ��I�ǡ�ABC�����ģ���BAC��ƽ���ߺ͡�ABC�����Բ�ཻ�ڵ�D��BD��ID�����Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
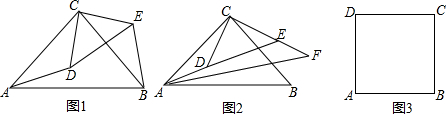
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
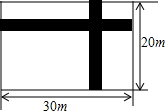 �ڿ�Ϊ20�ס���Ϊ30�ľ��ε�����������ͬ�����ĵ�·�����²�����Ϊ���أ������������Ҫ551��2��������·��ӦΪ���٣�
�ڿ�Ϊ20�ס���Ϊ30�ľ��ε�����������ͬ�����ĵ�·�����²�����Ϊ���أ������������Ҫ551��2��������·��ӦΪ���٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com