
| A. | (1,1) | B. | (-1,$\sqrt{3}$) | C. | (-2,-1) | D. | ($\sqrt{2}$,-2) |
分析 根据点的坐标性质结合勾股定理得出斜边长,进而得出点与⊙O关系.
解答 解:如图所示: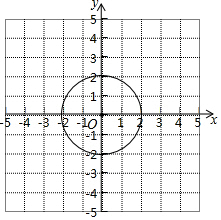
A、(1,1)点构成直角三角形的斜边为$\sqrt{2}$,小于2,故不在⊙O上,故此选项错误;
B、(-1,$\sqrt{3}$)点构成直角三角形的斜边为2,等于2,故在⊙O上,故此选项正确;
C、(-2,-1)点构成直角三角形的斜边为$\sqrt{5}$,大于2,故不在⊙O上,故此选项错误;
D、($\sqrt{2}$,-2)点构成直角三角形的斜边为$\sqrt{6}$,大于2,故不在⊙O上,故此选项错误;
故选:B.
点评 此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r,②点P在圆上?d=r,③点P在圆内?d<r.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,从一块直径是6m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
如图,从一块直径是6m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.| A. | $\frac{3\sqrt{30}}{4}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{30}$ | D. | 2$\sqrt{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+17=2 | B. | 3x-17=2 | C. | 3x-2=17 | D. | 3x+2=17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,四方形OABC内一点B的坐标是(5,4),P是线段BC上的点,将△ABP沿AP翻折,点B恰好落在x轴上的B′处.
如图,在平面直角坐标系中,四方形OABC内一点B的坐标是(5,4),P是线段BC上的点,将△ABP沿AP翻折,点B恰好落在x轴上的B′处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
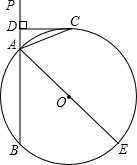 如图所示,已知直线PA交☉O于A、B两点,AE是☉O的直径,C为☉O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂直为D.
如图所示,已知直线PA交☉O于A、B两点,AE是☉O的直径,C为☉O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂直为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com