
��2013��㶫÷��10�֣���ͼ����֪������y=2x2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
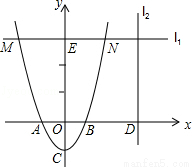
��1��д����A��B��CΪ����������������
��2������E��0��6������x��ƽ�е�ֱ��l1���������ཻ��M��N���㣨��M�ڵ�N����ࣩ����MNΪһ�ߣ��������ϵ���һ��PΪ��һ������ƽ���ı��Σ���ƽ���ı��ε����Ϊ8ʱ�������P�����ꣻ
��3������D��m��0��������m��1������x�ᴹֱ��ֱ��l2����һ��Q����Q�ڵ�һ���ޣ���ʹ����Q��D��BΪ����������κ���B��C��OΪ��������������ƣ����߶�QD�ij����ú�m�Ĵ���ʽ��ʾ����
�⣺��1����y=2x2��2���൱y=0ʱ��2x2��2=0��x=��1��
���A����������1��0������B��������1��0����AB=2��
�ֵ�x=0ʱ��y=��2�����C������Ϊ��0����2����OC=2��
��S��ABC= AB•OC=
AB•OC= ��2��2=2��
��2��2=2��
��2����y=6����y=2x2��2����2x2��2=6��x=��2��
���M����������2��6������N��������2��6����MN=4��
��ƽ���ı��ε����Ϊ8����MN���ϵĸ�Ϊ��8��4=2��
��P��������Ϊ6��2��
�ٵ�P��������Ϊ6+2=8ʱ��2x2��2=8��x=��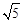 ��
��
���P��������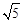 ��8����
��8����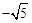 ��8����
��8����
�ڵ�P��������Ϊ6��2=4ʱ��2x2��2=4��x=�� ��
��
���P�������� ��4����
��4���� ��4����
��4����
������������ƽ���ı��ε����Ϊ8ʱ����P������Ϊ��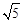 ��8����
��8����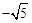 ��8����
��8���� ��4����
��4���� ��4����
��4����
��3���ߵ�B������Ϊ��1��0������C������Ϊ��0����2������OB=1��OC=2��
�ߡ�QDB=��BOC=90�㣬
����Q��D��BΪ����������κ���B��C��OΪ���������������ʱ�������������
��OB��BD���Ƕ�Ӧ��ʱ����OBC�ס�DBQ���� ����
����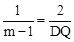 ��
��
���DQ=2��m��1��=2m��2��
��OB��QD���Ƕ�Ӧ��ʱ����OBC�ס�DQB����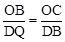 ����
���� ��
��
��� ��
��
�����������߶�QD�ij�Ϊ2m��2�� ��
��

����������1���ڶ��κ����Ľ���ʽy=2x2��2�У���y=0�����x=��1���õ�AB=2����x=0ʱ�����y=��2���õ�OC=2��Ȼ����������ε������ʽ���������ABC�������
��2���Ƚ�y=6����y=2x2��2�����x=��2���õ���M���N�����꣬��MN=4������ƽ���ı��ε������ʽ�õ�MN���ϵĸ�Ϊ2����P��������Ϊ8��4��������������ۣ��ٵ�P��������Ϊ8ʱ����y=8����y=2x2��2�����x��ֵ���õ���P�����ꣻ�ڵ�P��������Ϊ4ʱ����y=4����y=2x2��2�����x��ֵ���õ���P�����ꡣ
��3�����ڡ�QDB=��BOC=90�㣬������Q��D��BΪ����������κ���B��C��OΪ���������������ʱ��������������ۣ���OB��BD���Ƕ�Ӧ�ߣ���OB��QD���Ƕ�Ӧ������������������������ζ�Ӧ�߳ɱ�����ʽ�������QD�ij��ȼ��ɡ�
���㣺���κ����ۺ��⣬�����ϵ�������뷽�̵Ĺ�ϵ�������ε������ʽ��ƽ���ı��ε��ж������������ε��ж�������˼���Ӧ�á�


 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��㶫÷�ݾ�����ѧ�������棩 ���ͣ������
��2013��㶫÷��8�֣���ͼ�����ı���ABFC�У���ACB=90�㣬BC�Ĵ�ֱƽ����EF��BC�ڵ�D����AB���E����CF=AE��

��1����֤���ı���BECF�����Σ�
��2�����ı���BECFΪ�����Σ����A�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��㶫÷�ݾ�����ѧ�������棩 ���ͣ������
��2013��㶫÷��8�֣�Ϊ���軷��������������г����ũ�壬ij���ί������ڴ��������ֲA��B������ľ����Ҫ��������������1000�ã�A��B��������������Ϣ�����
|
|
���ۣ�Ԫ/�ã� |
�ɻ��� |
ֲ���ѣ�Ԫ/�ã� |
|
A |
20 |
90% |
5 |
|
B |
30 |
95% |
5 |
�蹺��A������x�ã��̻�������ܷ���ΪyԪ������������⣺
��1��д��y��Ԫ����x���ã�֮��ĺ�����ϵʽ��
��2��������������ֲ��ɻ���925�ã����̻�������ܷ�����Ҫ����Ԫ��
��3�����̻�������ܷ��ò�����31000Ԫ�������ɹ���B��������ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��㶫÷�ݾ�����ѧ�������棩 ���ͣ������
��2013��㶫÷��8�֣���ͼ���ھ���ABCD�У�AB=2DA���Ե�AΪԲ�ģ�ABΪ�뾶��Բ����DC�ڵ�E����AD���ӳ����ڵ�F����DA=2��

��1�����߶�EC�ij���
��2����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��㶫÷�ݾ�����ѧ�������棩 ���ͣ������
��2013��㶫÷��8�֣���֪��һ�κ���y=x+1��ͼ���뷴��������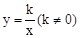 ��ͼ������A��a��2����
��ͼ������A��a��2����
��1����a��ֵ�������������ı���ʽ��
��2���жϵ�B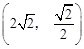 �Ƿ��ڸ÷�����������ͼ���ϣ���˵�����ɣ�
�Ƿ��ڸ÷�����������ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com