
分析 根据一元二次方程根的情况与判别式△=4m+8的关系确定m的取值.
(1)当4m+8>0时,方程有两个不相等的实数根;
(2)当4m+8=0时,方程有两个相等的实数根;
(3)当4m+8<0时,方程没有实数根.
解答 解:$\frac{1}{4}$x2+(m+2)x+m2=4,
$\frac{1}{4}$x2+(m+2)x+m2-4=0
△=(m+2)2-4×$\frac{1}{4}$(m2-4)=4m+8.
(1)当4m+8>0,m>-2时,方程有两个不相等的实数根;
(2)当4m+8=0,m=-2时,方程有两个相等的实数根;
(3)当4m+8<0,m<-2时,方程没有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,BO、CO分别是△ABC的外角平分线.
如图,BO、CO分别是△ABC的外角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 160万辆 | B. | 170万辆 | C. | 180万辆 | D. | 200万辆 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5<-3<$\frac{1}{2}$<0 | B. | 13<-5<$\frac{1}{2}$<0 | C. | -3<-5<0<$\frac{1}{2}$ | D. | -5<-3<0<$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
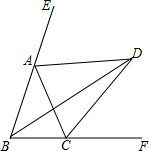 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com