
【题目】如图1,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB点E,DF⊥BC于点F.将∠EDF绕点D顺时针旋转α°(0<α<180),其两边的对应边DE′、DF′分别与直线AB、BC相交于点G、P,如图2.连接GP,当△DGP的面积等于3![]() 时,则α的大小为( )
时,则α的大小为( )

A. 30 B. 45 C. 60 D. 120
【答案】C
【解析】分析题目根据AB∥DC,∠BAD=60°,可得∠ADC的度数;
利用∠ADE=∠CDF=30°,可得∠EDF的度数,当∠EDF顺时针旋转时,由旋转的性质可知:∠EDG=∠FDP,∠GDP=∠EDF=60°,根据全等三角形的判定方法证明△DEG≌△DFP;
然后全等三角形的性质可得DG=DP,即可得出△DGP为等边三角形,利用面积和cos∠EDG可得∠EDG的度数,同理可得结论.
∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF=![]() ,∠DEG=∠DFP=90°,
,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
![]() ,
,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP为等边三角形,
∴△DGP的面积=![]() DG2=3
DG2=3![]() ,
,
解得,DG=2![]() ,
,
则cos∠EDG=![]() =
=![]() ,
,
∴∠EDG=60°,
∴当顺时针旋转60°时,△DGP的面积等于3![]() ,
,
故选:C.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
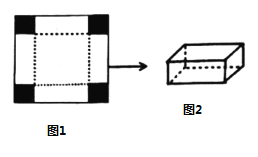
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() ,直接写出用只含字母
,直接写出用只含字母![]() 的式子表示这个盒子的高为______
的式子表示这个盒子的高为______![]() ,底面积为______
,底面积为______![]() ,盒子的容积
,盒子的容积![]() 为______
为______![]() ,
,
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
填空:①![]() ______,
______,![]() ______;
______;
②由表格中的数据观察可知当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中:①90°﹣∠α;②∠β﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠β﹣∠α)其中正确的有( )
(∠β﹣∠α)其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
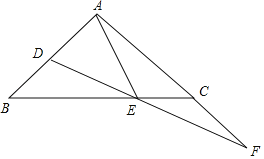
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
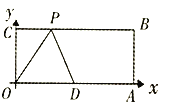
【题目】已知,如图,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 为矩形,
为矩形,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上运动,当
上运动,当![]() 是腰长为5的等腰三角形,则
是腰长为5的等腰三角形,则![]() 点的坐标为_________________________。
点的坐标为_________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
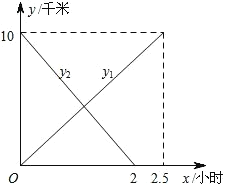
【题目】某中学九年级甲、乙两班商定举行一次远足活动,![]() 、
、![]() 两地相距10千米,甲班从
两地相距10千米,甲班从![]() 地出发匀速步行到
地出发匀速步行到![]() 地,乙班从
地,乙班从![]() 地出发匀速步行到
地出发匀速步行到![]() 地.两班同时出发,相向而行.设步行时间为
地.两班同时出发,相向而行.设步行时间为![]() 小时,甲、乙两班离
小时,甲、乙两班离![]() 地的距离分别为
地的距离分别为![]() 千米、
千米、![]() 千米,
千米,![]() 、
、![]() 与
与![]() 的函数关系图象如图所示,根据图象解答下列问题:
的函数关系图象如图所示,根据图象解答下列问题:
(1)直接写出![]() 、
、![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离![]() 地多少千米?
地多少千米?
(3)甲、乙两班相距4千米时所用时间是多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com