
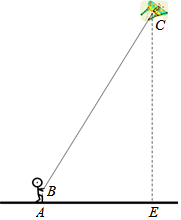
 小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,$\sqrt{3}$≈1.732)
小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,$\sqrt{3}$≈1.732) 分析 过点B作BD⊥CE于点D,由锐角三角函数的定义求出CD的长,根据CE=CD+DE即可得出结论.
解答 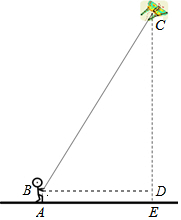 解:过点B作BD⊥CE于点D,
解:过点B作BD⊥CE于点D,
∵AB⊥AE,DE⊥AE,BD⊥CE,
∴四边形ABDE是矩形,
∴DE=AB=1.5米.
∵BC=40米,∠CBD=60°,
∴CD=BC•sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$,
∴CE=CD+DE=20$\sqrt{3}$+1.5≈20×1.73+1.5≈36.1(米).
答:此时风筝离地面的高度CE是36.1米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
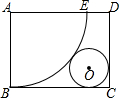 如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.
如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | 2 | D. | ±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com