
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпyЃН![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЈmЮЊГЃЪ§ЃЌЧвmЃО0ЃЉОЙ§ЕуcЃЈ0ЃЌЉ
ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЈmЮЊГЃЪ§ЃЌЧвmЃО0ЃЉОЙ§ЕуcЃЈ0ЃЌЉ![]() ЃЉЃЌгыxжсНЛгкЕуAЁЂBЃЈЕуAЮЛгкЕуBЕФзѓВрЃЉЃЎ
ЃЉЃЌгыxжсНЛгкЕуAЁЂBЃЈЕуAЮЛгкЕуBЕФзѓВрЃЉЃЎ
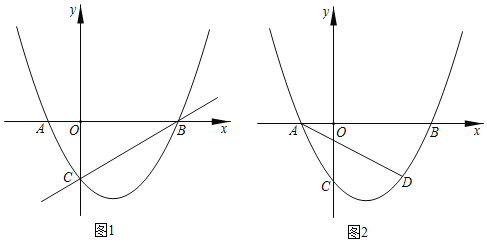
ЃЈ1ЃЉЧыжБНгаДГіmЕФжЕМАЕуAЁЂЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЧыФуЬНОПЃКдкжБЯпBCЩЯЪЧЗёДцдкЕуPЃЌЪЙвдPЁЂAЁЂBЮЊЖЅЕуЕФШ§НЧаЮгыЁїBOCЯрЫЦЃПШєДцдкЃЌЧыЧѓГіAPЕФГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЕуDЃЈ2ЃЌЉ![]() ЃЉЃЌСЌНгADЃЌХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙЁЯBAQЃН2ЁЯBADЃЌШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЉЃЌСЌНгADЃЌХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙЁЯBAQЃН2ЁЯBADЃЌШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉmЃН![]() ЃЌAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉДцдкЃЌAPЕФГЄЮЊ2Лђ
ЃЌAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉДцдкЃЌAPЕФГЄЮЊ2Лђ![]() ЃЛЃЈ3ЃЉДцдкЃЌЕуQЕФзјБъЮЊЃЈ0ЃЌЉ
ЃЛЃЈ3ЃЉДцдкЃЌЕуQЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЛђЃЈ6ЃЌ7
ЃЉЛђЃЈ6ЃЌ7![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуCЕФзјБъДњШыНтЮіЪНyЃН![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉМДПЩЧѓГіmЕФжЕЃЌСюyЃН0ЃЌМДПЩЧѓГіAЃЌBЕФКсзјБъЃЛ
ЃЈx+1ЃЉЃЈxЉ3ЃЉМДПЩЧѓГіmЕФжЕЃЌСюyЃН0ЃЌМДПЩЧѓГіAЃЌBЕФКсзјБъЃЛ
ЃЈ2ЃЉЗжЧщПіЬжТлЃЌЕБвдЕуPЮЊжБНЧЖЅЕуЪБЃЌжЄЁїABCЮЊжБНЧШ§НЧаЮЃЌЧвгыЁїBOCЯрЫЦЃЌЫљвдЕуPгыЕуCжиКЯЃЛЕБвдЕуAЮЊжБНЧЖЅЕуЪБЃЌЙ§ЕуAзїxжсЕФДЙЯпЃЌНЛBCгкЕуPЃЌгЩЯрЫЦЕФаджЪЧѓГіAPЕФГЄЖШМДПЩЃЛЕБвдЕуBЮЊжБНЧЖЅЕуЪБЃЌВЛДцдкЃЛ
ЃЈ3ЃЉЗжЧщПіЬжТлЃЌЯШЧѓГіЁЯBADЃН30ЁуЃЌЕБЕуQдкxжсЯТЗНЪБЃЌЧѓГіЁЯBACЃН60ЁуЃЌдђЕуQгыЕуCжиКЯЃЛЕБЕуQдкxжсЩЯЗНЪБЃЌзїЕуCЙигкxжсЕФЖдГЦЕуEЃЌжБЯпAEгыХзЮяЯпдкxжсЩЯЗНЕФНЛЕуМДЮЊЕуQЃЎ
ЃЈ1ЃЉНЋЕуCЃЈ0ЃЌЉ![]() ЃЉДњШыyЃН
ЃЉДњШыyЃН![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌ
ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌ
ЕУЃЌmЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊЃКyЃН![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉЃН
ЃЈx+1ЃЉЃЈxЉ3ЃЉЃН![]() x2Љ
x2Љ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
ЕБyЃН0ЪБЃЌx1ЃНЉ1ЃЌx2ЃН3ЃЌ
ЁрAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉДцдкЕуPЃЌРэгЩШчЯТЃК
ЂйдкХзЮяЯпyЃН![]() x2Љ
x2Љ![]() xЉ
xЉ![]() жаЃЌ
жаЃЌ
ЕБxЃН0ЪБЃЌyЃНЉ![]() ЃЌ
ЃЌ
ЁрCЃЈ0ЃЌЉ![]() ЃЉЃЌOCЃН
ЃЉЃЌOCЃН![]() ЃЌ
ЃЌ
ЁрAC2ЃНAO2+CO2ЃН4ЃЌBC2ЃНBO2+CO2ЃН12ЃЌ
гжЁпAB2ЃН42ЃН16ЃЌ
ЁрAC2+BC2ЃНAB2ЃЌ
ЁрЁїABCЪЧжБНЧШ§НЧаЮЃЌ
ЁрЁЯACBЃНЁЯCOBЃН90ЁуЃЌ
гжЁпЁЯOBCЃНЁЯCBAЃЌ
ЁрЁїBOCЁзЁїBCAЃЌ
МДЕуPгыЕуCжиКЯЃЌ
ЁрAPЃНACЃН![]() ЃН2ЃЛ
ЃН2ЃЛ
ЂкЙ§ЕуAзїAPЁЭxжсЃЌНЛжБЯпBCгкЕуPЃЌ
дђAPЁЮOCЃЌ
ЁрЁїBAPЁзЁїBOCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAPЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌAPЕФГЄЮЊ2Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкЕуQЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌЙ§ЕуDзїDHЁЭxжсгкЕуHЃЌ
дђHЃЈ2ЃЌ0ЃЉЃЌ
ЂйЕБЕуQдкxжсЯТЗНЪБЃЌ
DHЃН![]() ЃЌAHЃН3ЃЌ
ЃЌAHЃН3ЃЌ
ЁрдкRtЁїAHDжаЃЌ
tanЁЯBADЃН![]() ЃЌ
ЃЌ
ЁрЁЯBADЃН30ЁуЃЌ
дкRtЁїAOCжаЃЌ
tanЁЯBACЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁЯBACЃН60ЁуЃЌ
ЁрЁЯBACЃН2ЁЯBADЃЌ
ЁрЕуQгыЕуCжиКЯЃЌ
ЁрQ1ЃЈ0ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБЕуQдкxжсЩЯЗНЪБЃЌ
зїЕуCЙигкxжсЕФЖдГЦЕуEЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дђЁЯEABЃНЁЯCABЃН60ЁуЃН2ЁЯBADЃЌ
дђжБЯпAEгыХзЮяЯпдкxжсЩЯЗНЕФНЛЕуМДЮЊЕуQЃЌ
ЩшжБЯпAEЕФНтЮіЪНЮЊyЃНkx+![]() ЃЌ
ЃЌ
НЋЕуAЃЈЉ1ЃЌ0ЃЉДњШыЃЌЕУ
kЃН![]() ЃЌ
ЃЌ
ЁрyAEЃН![]() x+
x+![]() ЃЌ
ЃЌ
СЊСЂЃЌЕУ![]() x+
x+![]() ЃН
ЃН![]() x2Љ
x2Љ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
НтЕУЃЌx1ЃНЉ1ЃЌx2ЃН6ЃЌ
ЁрQ2ЃЈ6ЃЌ7![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЕуQЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЛђЃЈ6ЃЌ7
ЃЉЛђЃЈ6ЃЌ7![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
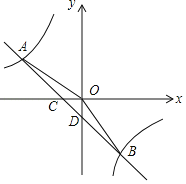
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНax+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ4ЃЉЃЌСЌНгAOЃЌAOЃН5ЃЌsinЁЯAOCЃН
ЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ4ЃЉЃЌСЌНгAOЃЌAOЃН5ЃЌsinЁЯAOCЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгOBЃЌЧѓЁїAOBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЛ§МЋЯьгІаТОЩЖЏФмзЊЛЛ.ЬсИпЙЋЫООМУаЇвц.ФГПЦММЙЋЫОНќЦкбаЗЂГівЛжжаТаЭИпПЦММЩшБИЃЌУПЬЈЩшБИГЩБОМлЮЊ30ЭђдЊ,ОЙ§ЪаГЁЕїбаЗЂЯж,УПЬЈЪлМлЮЊ40ЭђдЊЪБ,ФъЯњЪлСПЮЊ600ЬЈ;УПЬЈЪлМлЮЊ45ЭђдЊЪБ,ФъЯњЪлСПЮЊ550ЬЈ.МйЖЈИУЩшБИЕФФъЯњЪлСПy(ЕЅЮЛ:ЬЈ)КЭЯњЪлЕЅМл![]() (ЕЅЮЛ:ЭђдЊ)ГЩвЛДЮКЏЪ§ЙиЯЕ.
(ЕЅЮЛ:ЭђдЊ)ГЩвЛДЮКЏЪ§ЙиЯЕ.
(1)ЧѓФъЯњЪлСП![]() гыЯњЪлЕЅМл
гыЯњЪлЕЅМл![]() ЕФКЏЪ§ЙиЯЕЪН;
ЕФКЏЪ§ЙиЯЕЪН;
(2)ИљОнЯрЙиЙцЖЈ,ДЫЩшБИЕФЯњЪлЕЅМлВЛЕУИпгк70ЭђдЊ,ШчЙћИУЙЋЫОЯыЛёЕУ10000ЭђдЊЕФФъРћШѓ.дђИУЩшБИЕФЯњЪлЕЅМлгІЪЧЖрЩйЭђдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
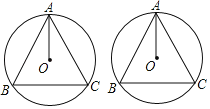
ЁОЬтФПЁПШчЭМЃЌABЃЌACЪЧЁбOЕФСНЬѕЯвЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКAOЦНЗжЁЯBACЃЛ
ЃЈ2ЃЉШєABЃН4![]() ЃЌBCЃН8ЃЌЧѓАыОЖOAЕФГЄЃЎ
ЃЌBCЃН8ЃЌЧѓАыОЖOAЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
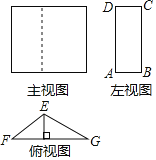
ЁОЬтФПЁПФГМИКЮЬхЕФШ§ЪгЭМШчЭМЫљЪОЃЌвбжЊдкЁїEFGжаЃЌFGЃН18cmЃЌEGЃН12cmЃЌЁЯEGFЃН30ЁуЃЛдкОиаЮABCDжаЃЌADЃН16cmЃЎ
ЃЈ1ЃЉЧыИљОнШ§ЪгЭМЫЕУїетИіМИКЮЬхЕФаЮзДЃЎ
ЃЈ2ЃЉЧыФуЧѓГіABЕФГЄЃЛ
ЃЈ3ЃЉЧѓГіИУМИКЮЬхЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОбаЗЂСЫвЛПюГЩБОЮЊ50дЊЕФаТаЭЭцОпЃЌЭЖЗХЪаГЁНјааЪдЯњЪлЃЎЦфЯњЪлЕЅМлВЛЕЭгкГЩБОЃЌАДееЮяМлВПУХЙцЖЈЃЌЯњЪлРћШѓТЪВЛИпгк90%ЃЌЪаГЁЕїбаЗЂЯжЃЌдквЛЖЮЪБМфФкЃЌУПЬьЯњЪлЪ§СПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЫљЪОЃК
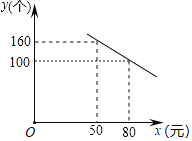
ЃЈ1ЃЉИљОнЭМЯѓЃЌжБНгаДГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУЙЋЫОвЊЯыУПЬьЛёЕУ3000дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊ
ЃЈ3ЃЉЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋАыОЖЮЊ3ЕФдВаЮжНЦЌЃЌАДЫГађелЕўСНДЮЃЌелЕўКѓЕФЛЁABКЭЛЁBCЖМОЙ§дВаФOЃЎ
ЃЈ1ЃЉСЌНгOAЁЂOBЃЌЧѓжЄЃКЁЯAOBЃН120ЁуЃЛ
ЃЈ2ЃЉЭМжавѕгАВПЗжЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
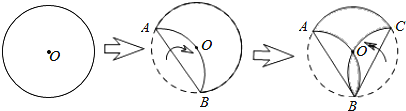
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌЁЯBAC=60ЁуЃЌШєЁбOЕФАыОЖ0CЮЊ2ЃЌдђЯвBCЕФГЄЮЊЃЈЁЁЁЁЃЉ
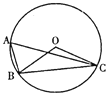
A. 1
B. ![]()
C. 2
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дк![]() жаЃЌЕу
жаЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯ,Чв
ЩЯ,Чв![]() ЮЊБп
ЮЊБп![]() бгГЄЯпЩЯвЛЕу,СЌНг
бгГЄЯпЩЯвЛЕу,СЌНг![]() ,дђЭМжагы
,дђЭМжагы![]() ЯрЫЦЕФШ§НЧаЮга( )Иі
ЯрЫЦЕФШ§НЧаЮга( )Иі
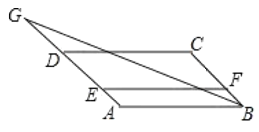
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com