
 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.分析 (1)利用边OA比OC大2且面积为15,可列方程求得OA、OC;
(2)分别以点A、点O为圆心,OA为半径画圆,与BC的交点即为满足条件的P点,结合勾股定理可求得这些点的坐标.
解答 (1)解:在矩形OABC中,设OC=x,则OA=x+2,
∴x(x+2)=15,
∴x1=3,x2=-5,
∴x2=-5(不合题意,舍去),
∴OC=3,OA=5;
(2)解:存在.
①当AO=AP时,如图,以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H=OC=3;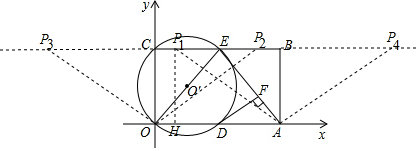
∵APl=OA=5,
∴AH=4,
∴OH=l,
求得点P1(1,3)同理可得:P4(9,3);
②当OA=OP时,同上可求得P2(4,3),P3(-4,3),
∴在直线BC上,除了E点外,既存在⊙O′内的点P,又存在⊙O′外的点P使△AOP为等腰三角形,
其坐标为(1,3)或(9,3)或(4,3)或(-4,3).
点评 本题主要考查矩形的性质、等腰三角形的判定及勾股定理等知识的综合应用.在(1)中注意方程思想的应用;在(2)中注意利用圆上的点到圆心的距离相等的特点找出满足条件的点的位置.本题综合性较强,待查知识点较多,在平时的学习中要注意知识的灵活运用.


科目:初中数学 来源: 题型:选择题
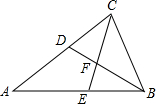 如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 品牌 | 月租费 | 本地话费(元/分钟) | 长途话费(元/分钟) |
| 全球通 | 13元 | 0.35 | 0.15 |
| 神州行 | 0元 | 0.60 | 0.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
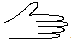 -3x+2=x2-5x+1.
-3x+2=x2-5x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
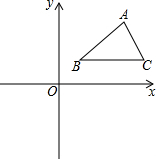 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
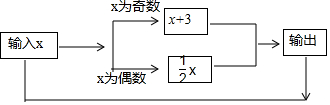
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com